最近连续被问到两三次, 可惜时间紧张没能帮上什么忙, 这里就记一下解决过程吧

小明向他的女友仙仙求婚, 在求婚戒指上刻了一个大大的爱心. 仙仙看到爱心想考验一下小明, 出了一道题. 方程 $(x^2 + y^2 - 1)^3 -x^2y^3 = 0$ 能画出一个美丽的爱心, 现在给定一个点 $(X, Y)$, 其中 $ X \sim N(\mu_1, \sigma_1^2) $, $ Y \sim N(\mu_2, \sigma_2^2) $, 这个点在这个爱心里面的概率是多少? 精确到0.1

这是一道概率题, 起初想到的是直接在心形线内对概率积分, 后来经过同学的提醒才知道可以直接用实验模拟. 现在介绍一下这两种方法

蒙特卡洛方法

其实就是一个单变量概率模拟, 直接按给定的概率$(u1, u2, s1, s2)$生成坐标, 然后判断一下在不在心形线内部, 进行足够迭代次数之后就可以统计概率了. 很直观的做法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

import numpy as np

def calc_prob(u1, u2, s1, s2, iter_num):
    in_circle = 0
    for i in range(iter_num):
        x = np.random.normal(u1, s1)
        y = np.random.normal(u2, s2)
        if ((x**2 + y**2 - 1)**3 - (x**2) * (y**3)) < 0:
            in_circle += 1
    return float(in_circle)/iter_num

if __name__ == '__main__':
    print calc_prob(0,0,1,1,10000)

• 输出结果大约收敛在0.424

二重积分计算

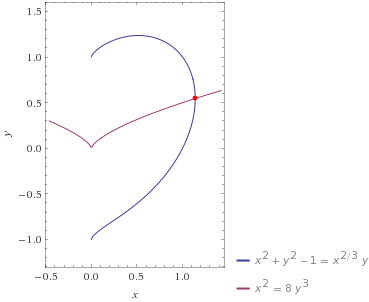
首先观察一下曲线:

1. 看右半边显然曲线是右凸的, 为了避免分段, 决定先从y轴再从x轴积分

2. 为了取得x轴的上下限. 由于正态分布的中心对称性, x从0开始积分就行了.至于上限, 获得了方程之后求x的极值即可:

   1. 化简方程为: $x^2 + y^2 - 1 = x^{2/3}y$, 这是心形线的右半部分
   2. 隐函数求导, 解出$\frac{dx}{dy}$: 3. $ 2xdx + 2ydy = \frac{2}{3}x^{-\frac{1}{3}}ydx + x^{\frac{2}{3}}dy$ 4. $(2x-\frac{2}{3}x^{-\frac{1}{3}}y) \frac{dx}{dy} = x^{\frac{2}{3}} - 2y$ 5. 令$\frac{dx}{dy} = 0$, 得到$x^2 = 8y^3$, 联立方程组解得上限$x_{max} \approx 1.13903$

3. y轴的上下限容易计算, 直接求解化简的方程就行了.

   1. $ y_{min} = \frac{1}{2}(x^{\frac{2}{3}} - \sqrt{x^{\frac{4}{3}} - 4 x^2 + 4)} $
   2. $ y_{max} = \frac{1}{2}(x^{\frac{2}{3}} + \sqrt{x^{\frac{4}{3}} - 4 x^2 + 4)} $

4. 最后求积分即可

$$ \frac{1}{\pi\sigma_1\sigma_2} \int_{x=0}^{x=1.139} \int_{y_{min}}^{y_{max}} e^{-\frac{(x - \mu_1)^2}{2\sigma_1^2} - \frac{(y- \mu_2)^2}{2\sigma_2^2}} dydx $$

• 将第一种方法中的参数代入之后得到结果如下

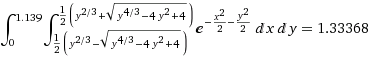
• 计算$\frac{1.33368}{\pi} = 0.4245$, 得到的结果相似.

后记

1. x的最大值大概在哪?

2. x的解析解是什么? $$ \frac{1}{8 \sqrt{ \frac{3}{193 + \sqrt[3]{55873 - 1536 \sqrt{1299}} + \sqrt[3]{55873 + 1536 \sqrt{1299}}}}} $$

3. 真正的心形线(Cardioid)长这个样子, 曲线方程也优美得多. 这道题使用数学手段计算毫无美感. 阿里的HRG里没有强迫症改一下嘛w

4. 把女友换成男友, 这个题目的剧情会更合理一些(たぶん