Hidden Markov Model

0. 定义
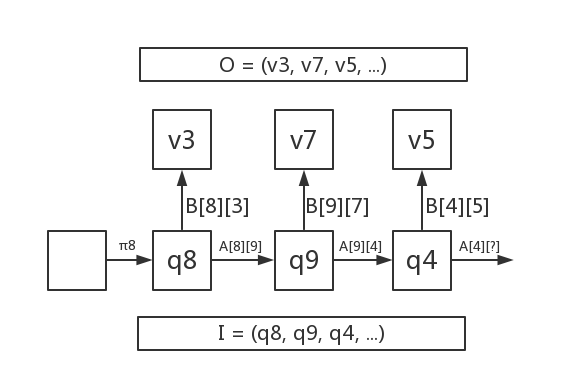
如图所示, 线性HMM由状态$V$和观察$Q$的序列$I$和$O$组成, 其中$I$是马尔科夫链(Markov Chain). 状态之间通过转移矩阵$A$(transition)决定状态转移的概率分布, 每一时间步的状态通过观察矩阵$B$(emission)决定观察结果的概率分布.而状态一般是未知的.
0.0 符号表
| 符号 | 含义 | 备注 |
|---|---|---|
| $Q = \lbrace q_1, q_2, \cdots, q_{N_Q} \rbrace$ | 状态(state) | |
| $I = (I_1, I_2, \cdots, I_T)$ | 状态序列 | $I_t \in Q$ |
| $V = \lbrace v_1, v_2, \cdots, v_{N_V} \rbrace$ | 观察(observation) | |
| $O = (o_1, o_2, \cdots, o_T )$ | 观察序列 | $o_t \in V$ |
| $A_{ij} \in R^{N_Q \times N_Q}$ | 状态转移矩阵 | $P(I_t = q_j \lvert I_{t-1} = q_i)$ |
| $B_{q_i}(v_j ) \in R^{N_Q \times N_V}$ | 观测概率矩阵(emission) | $P(o_t = v_j \lvert I_t = q_i)$ |
| $\pi \in R^{N_Q}$ | 初始状态分布 | $P(I_1 = q_i)$ |
| $\lambda=(\pi, A, B)$ | 模型参数 | HMM的参数由$\lambda$组成 |
- 状态转移矩阵代表了从状态$q_i$转移到$q_j$的概率
- 观测概率矩阵代表了从状态$q_i$观察到输出$v_j$的概率
0.1 基本假设
- 一阶齐次Markov假设: 任意时刻的状态$I_t$只依赖于前一时刻的状态$I_{t-1}$
- 任意时刻的观察$O_t$只依赖于该时刻的状态$I_t$
0.2 基本问题
HMM作为一个生成模型, 也涉及概率计算, 学习问题和预测问题(也叫decoding)
- 概率计算: 已知$\lambda$, 求$P(O|\lambda)$
- 学习问题: 已知$O$, 求$arg\max\limits_{\lambda}P(O|\lambda)$
- 预测问题: 已知$O, \lambda$, 求$arg\max\limits_{I}P(I|O, \lambda)$
1. 概率计算
已知$\lambda=(A, B, \pi)$, 计算观测序列$O$出现的概率$P(O|\lambda)$.
1.1 直接计算
在已知$O$的情况下, 需要知道所有可能的状态序列$I$, 对所有状态序列与观察结果的联合概率分布求和.
- 状态序列$(I_1, I_2, \cdots, I_T)$的概率为 $$ P(I) = \pi_{I_1} \prod_{t=2}^{T} A_{I_{t-1} I_t} \tag{1.1.1} $$
- 状态序列为$I$, 观测序列为$O$的概率为 $$ \begin{align} P(O, I) &= P(O | I)P(I) \\ &= \pi_{I_1}B_{I_1}(o_1) \prod_{t=2}^{T} A_{I_{t-1} I_t}B_{I_t}(o_t) \end{align} \tag{1.1.2} $$
- 对所有可能的$I$求和, 时间复杂度为$O(N_V^T)$, 每次计算时间复杂度为$O(T)$, 总复杂度为$O(TN_V^T)$ $$ P(O) = \sum_I P(O, I) $$
1.2 前向算法
对所有的$I$求和, 由于每一步$I$都可能属于$Q$中的任何一个, 相当于在以下$N \times T$矩阵中寻找从左边到右边的所有路径的概率和. $$ \begin{align} &\begin{bmatrix} o_1 & o_2 & \cdots & o_T\\ \end{bmatrix} \\ &\begin{bmatrix} q_1 & q_1 & \cdots & q_1 \\ q_2 & q_2 & \cdots & q_2 \\ \vdots & \vdots & \ddots & \vdots \\ q_N & q_N & \cdots & q_N \\ \end{bmatrix} \end{align} \tag{1.2.1} $$
(示意图, 侵删)
对所有的路径求和涉及到大量的重复运算. 假设已经计算出了$(I_1, I_2, \cdots, I_t=q_t)$的所有可能的路径的概率之和, 那么在计算$(I_1, I_2, \cdots, I_{t+1})$时, 所有经过节点$I_t=q_t$的路径即可复用之前的计算结果. 写成递推式即为: $$ \alpha_{t+1}(q_i) = \sum_{j=1}^N \alpha_t(q_j) A_{ji} \tag{1.2.2} $$ 输出是已知的, 可以求出给定输出的概率为: $$ \alpha_{t+1}(q_i) = B_{q_i}(o_{t+1})\sum_{j=1}^N \alpha_t(q_j) A_{ji} \tag{1.2.3} $$ 其中 $$\alpha_{t}(q_i) = P((o_1, o_2, \cdots, o_t), I_t=q_i)\tag{1.2.4}$$ 使用此式递推, 时间复杂度为$O(TN^2)$
1.3 后向算法
类似地定义后向算法. 假设已经计算出了$(I_t=q_i, I_{t+1}, \cdots, I_T)$的所有可能的路径的概率之和, 那么在计算$(I_{t-1}, I_t, \cdots, I_T)$时, 所有经过节点$I_t=q_t$的路径即可复用之前的计算结果. $$ \beta_{t-1}(q_i) = \sum_{j=1}^N A_{ij} \beta_{t}(q_j) B_{q_j}(o_{t}) \tag{1.3.1} $$ 其中 $$\beta_{t}(q_i) = P((o_{t+1}, o_{t+2}, \cdots, o_T), I_t=q_i)\tag{1.3.2}$$
1.4 小结
结合前向和后向算法的表达式, 可以发现 $$ P(O, I_t=q_i) = \alpha_{t}(q_i) \beta_{t}(q_i) \tag{1.4.1} $$ 给定输出$O$, 状态$I_t=q_i$的概率可以利用全概率公式得到: $$ \begin{align} \gamma_t(q_i)=P(I_t=q_i|O) &= \frac{P(O, I_t=q_i)}{P(O)} \\ &= \frac{P(O, I_t=q_i)}{\sum_j P(O, I_t=q_j)} \\ &= \frac{\alpha_{t}(I_t=q_i) \beta_{t}(I_t=q_i)}{\sum_j \alpha_{t}(I_t=q_j) \beta_{t}(I_t=q_j)} \end{align} \tag{1.4.2} $$ 类似方法可以求出给定输出$O$, 状态$I_t=q_i$, $I_{t+1}=q_j$的概率: $$ \begin{align} \xi_t(q_i, q_j) &= P(I_t=q_i, I_{t+1}=q_j|O) \\ &=\frac{P(I_t=q_i, I_{t+1}=q_j, O)}{P(O)} \\ &=\frac{P(I_t=q_i, I_{t+1}=q_j, O)}{\sum_i \sum_j P(I_t=q_i, I_{t+1}=q_j, O)} \end{align} \tag{1.4.3} $$ 其中$P(I_t=q_i, I_{t+1}=q_j, O)=\alpha_t(q_i)A_{ij}B_{q_j}(o_{t+1})\beta_{t+1}(q_j)$ $(1.4.1)$和$(1.4.3)$可以被用于化简学习问题的求解
2. 学习问题
2.1 Supervised: MLE
已知$I, O$, 求$A, B$的MLE, 直接用频数计算 $$ A_{ij} = \frac{\sum\limits_{t=1}^{T-1} I(I_t = q_i, I_{t+1} = q_j)}{\sum\limits_{t=1}^{T-1} \sum\limits_{j=1}^{N_Q} I(I_t = q_i, I_{t+1} = q_j)} \tag{2.1.1} $$
$$ B_{q_i}(v_j) = \frac{\sum\limits_{t=1}^{T-1} I(I_t = q_i, o_t = v_j)}{\sum\limits_{t=1}^{T-1} \sum\limits_{j=1}^{N_V} I(I_t = q_i, o_t = v_j)} \tag{2.1.2} $$
2.2 Non-Supervised: Baum-Welch
只知道$O$, 不知道$I$, 求$A, B$的MLE, 采用EM算法
- E步: 给定参数先验$\overline \lambda$, 计算Q函数 $$Q(\lambda, \overline \lambda) = \sum\limits_I P(I| O, \overline \lambda) logP(I, O | \lambda) \tag{2.2.1}$$
- M步: 求$Q(\lambda, \overline\lambda)$对$\lambda$的最大值 $$ \max\limits_{\lambda} \sum\limits_I P(I| O, \overline \lambda) logP(I, O | \lambda) \tag{2.2.2}$$
- $\overline \lambda = \lambda$, 重复1和2.
由于 $$ P(I | O, \overline \lambda) = \frac{P(I, O| \overline \lambda)}{P(O | \overline \lambda)} \tag{2.2.3} $$ 而优化目标是最大化$P(I, O | \lambda)$对$I$的期望,和$P(O | \overline \lambda)$无关 故可以用$P(I, O| \overline \lambda)$替代
其中 $$ P(I, O | \lambda) = \pi_{I_1} B_{I_1}(o_1)\prod\limits_{t=1}^{T-1} A_{I_{t}I_{t+1}}B_{I_{t+1}}(o_{t+1}) \tag{2.2.4} $$ 将$(2.2.4)$带入$(2.2.2)$, 使用拉格朗日乘子法可以求出$\lambda$
$$ \pi_{q_i} = \gamma_1(q_i) \\ A_{ij} = \frac{\sum\limits_{t=1}^{T-1}\xi_t(q_i, q_j)}{\sum\limits_{t=1}^{T-1} \gamma_t(q_i)} \\ B_{q_i}(v_j) = \frac{\sum\limits_{t=1}^{T-1} [\gamma_t(q_i) I(o_t=v_j)]}{\sum\limits_{t=1}^{T-1} \gamma_t(q_i)} \tag{2.2.5} $$
3. Decode
已知$\lambda=(A, B, \pi), O=(o_1, o_2, \cdots, o_T)$, 求使得$P(I|O,\lambda)$最大的状态序列$I$. 由于 $$P(I | O, \lambda) = \frac{P(I, O| \lambda)}{P(O | \lambda)}$$ 而$P(O | \lambda)$与状态序列$I$无关, 因此该问题等价于 $$ \begin{align} \max\limits_{I} P(I|O, \lambda) & \Leftrightarrow \max\limits_{I} P(I, O| \lambda) \\ & \Leftrightarrow \max\limits_{I} \prod\limits_{t=0}^{T-1} A_{I_{t}I_{t+1}}B_{I_{t+1}}(o_{t+1}) \end{align} \tag{3.1} $$ 其中为了简化计算, 令$A_{I_0I_1} = \pi_{I_1}$.
由此可见, 问题转化为在$(1.2.1)$中找到一条路径使得$(4.1)$最大. 可以使用类似于Dijkstra算法的动态规划, 只不过这里加权路径使用的是累乘计算. 该算法被称为Viterbi算法. 由于图是层次的, 因此比Dijkstra算法简单
3.1 Viterbi算法
- 初始化 $$ \delta_1(q_i) = \pi_{q_i} \\ \phi_1(q_i) = 0 \tag{3.1.1} $$
- 递推. 对$t=[2, T]$: $$ \delta_t(q_i) = \max\limits_{1 \leq j \leq N_Q} [\delta_{t-1}(q_j)A_{ji}] B_{q_i}(o_t) \\ \phi_t(q_i) = arg\max\limits_{1 \leq j \leq N_Q} [\delta_{t-1}(q_j)A_{ji}] \tag{3.1.2} $$
- 终止 $$ P = \max\limits_{1 \leq i \leq N_Q} \delta_T(q_i) \\ I_T = arg\max\limits_{1 \leq i \leq N_Q} \delta_T(q_i) \tag{3.1.3} $$
- 逆推最优状态序列. 对$t=T-1, T-2, \cdots, 1$ $$ I_t = \phi_{t+1}(I_{t+1}) \tag{3.1.4} $$
其中 $$ \delta_t(q_i)=\max\limits_{I_i \cdots I_{t-1}} P((I_1, I_2, \cdots, I_t=q_i), O | \lambda) \tag{3.1.5} $$ $\delta_t(q_i)$代表输出为$O$且以$q_i$结尾长度为$t$的任意状态序列的最大联合概率 $\phi_t(q_i)$代表$(3.1.5)$时的$I_{t-1}$, 顺着逆推即可得到概率最大路径
4. Python 实现
to be continued….