循环神经网络的前世今生

xiaoxuan

2018-01-29 2996 words 6 minutes

Contents

新年第一篇, 和永无止境的八月一样循环的神经网络(其实是存货

Standard RNN

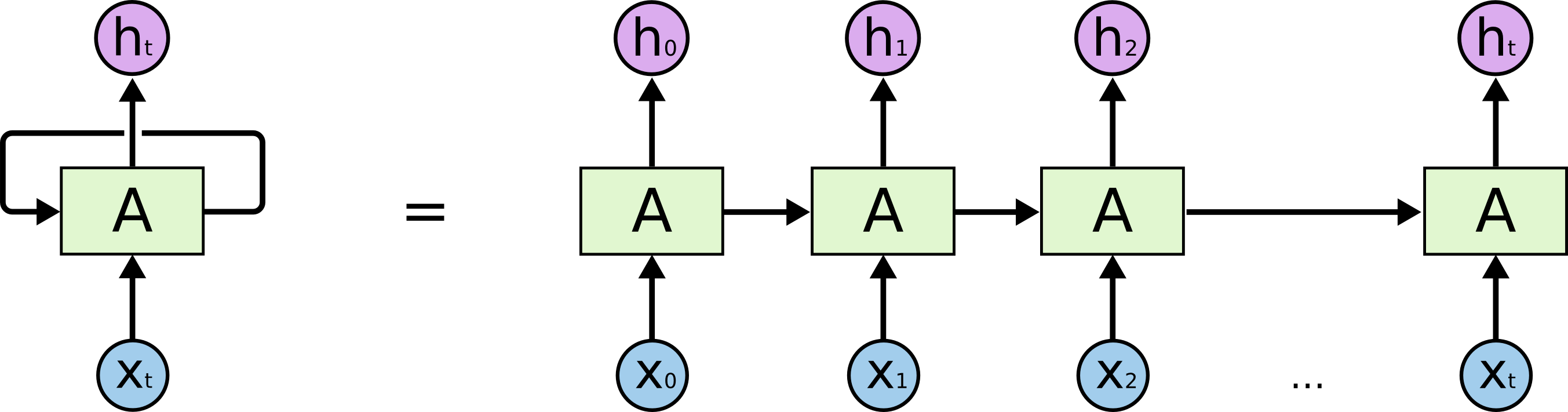
Standard RNN结构如上图, 主要涉及:

hidden state的更新
输出值y的计算

(本文忽略偏置项) $$ \begin{aligned} h^{(t)} &= tanh(Wx^{(t)} + Uh^{(t-1)}) \\ y^{(t)} &= softmax(Vh^{(t)}) \end{aligned} $$

LSTM

LSTM(Long Short-Term Memory)是RNN的变种, 他的诞生要追溯到1997年. Hochreiter S & Schmidhuber J (2000) 在Neural Computation上提出了该网络结构. 没错, 是Neural Computation XD LSTM意在解决RNN无法传递长程状态的缺陷, 其核心概念是Cell State

Calculate Cell State

利用cell state来携带长程信息, 记为$c^{(t)}$. 在当前时间步$t$利用输入$x^{(t)}$和前一步的$h^{(t-1)}$产生该时刻的长程信息${\hat c}^{(t)}$, 该层也可以称作cell state层: $$ \hat c^{(t)} = tanh(W_c x^{(t)} + U_c h^{(t-1)}) \tag{1.1} $$

Transmit Cell State

添加长程信息的频率应该是很低的, 因此设置输入门$g_{in}$挑选长程信息加入cell state: $g_{in} \otimes {\hat c}^{(t)}$
如果长程信息设为$c^{(t)} = c^{(t-1)} + g_{in} \otimes {\hat c}^{(t)}$, 总是保留旧信息$c^{(t-1)}$会让$c^{(t)}$迅速饱和导致梯度爆炸, 无法传递长程信息. 因此需要设置遗忘门$g_{f}$控制旧cell state的去留: $g_{f} \otimes c^{(t-1)}$ $$c^{(t)} = g_{f} \otimes c^{(t-1)} + g_{in} \otimes {\hat c}^{(t)} \tag{1.2}$$
最后利用输出门$g_{out}$从cell state中选择合适的输出: $$ h^{(t)} = g_{out} \otimes f(c^{(t)}) \tag{1.3}$$

Long Term & Short Term

什么是LSTM中的Long Term & Short Term?

回溯cell state的计算图, 发现$c^{(t)}$的更新只涉及到element wise乘法和加法, 梯度可以稳定传播, 属于长程(Long Term)信息
回溯hidden state的计算图, 发现$h^{(t)}$的计算取决于$c^{(t)} $, 而$c^{(t)}$的计算取决于$Uh^{(t-1)}$, 故反向传播需要跨越$U$. 和RNN一样易导致梯度消失, $h^{(t)}$属于短程(Short Term)信息

Input, Forget, Output Gate & Cell State

输入门, 遗忘门, 输出门和Cell State都是根据当前输入$x^{(t)}$和前一步输出$h^{(t-1)}$决定, 这是可以并行计算的四层神经网络, 他们的权重用下标加以区分 $$ \begin{aligned} \hat c^{(t)} &= tanh(W_c x^{(t)} + U_c h^{(t-1)}) \\ g_{in} &= sigmoid(W_i x^{(t)} + U_i h^{(t-1)}) \\ g_f &= sigmoid(W_f x^{(t)} + U_f h^{(t-1)}) \\ g_{out} &= sigmoid(W_o x^{(t)} + U_o h^{(t-1)}) \\ \end{aligned} \tag{1.4} $$

这四层网络可以直接用一个矩阵表示:

$$ \begin{aligned} \begin{bmatrix} {\hat c}_r^{(t)} \\ {\hat g}_{in}^{(t)} \\ {\hat g}_f ^{(t)} \\ {\hat g}_{out}^{(t)} \end{bmatrix} &= \begin{bmatrix} W_c & U_c \\ W_i & U_i \\ W_f & U_f \\ W_o & U_o \end{bmatrix} \cdot \begin{bmatrix} x^{(t)} \\ h^{(t-1)} \end{bmatrix} = W \cdot I^{(t)} \end{aligned} \tag{1.5} $$

其中${\hat c_r}^{(t)}$, $\hat g_{in}$, $\hat g_f$, $\hat g_{out}$代表被激活之前的仿射运算结果, 以下为简洁省略门的时间标记${(t)}$

Peephole Connection

四个门的开闭目前仅取决于当前输入$x^{(t)}$和前一步输出$h^{(t-1)}$, 而依上文所叙, $h^{(t-1)}$属于短程信息, 那么所有门控尤其是输出门并不能从长程信息中获益, 这不利于输出门保留长程信息. 因此将前一步的Cell State引入门单元的计算可以提高网络性能. 这项技术依然是LSTM的提出者3年后的工作, Gers & Schmidhuber (2000).

此时的计算方式为:

$$ \begin{aligned} \begin{bmatrix} {\hat c_r}^{(t)} \\ {\hat g_{in}}^{(t)} \\ {\hat g_f} ^{(t)} \\ {\hat g_{out}}^{(t)} \end{bmatrix} &= \begin{bmatrix} W_c & U_c & V_c \\ W_i & U_i & V_i \\ W_f & U_f & V_f \\ W_o & U_o & V_o \end{bmatrix} \cdot \begin{bmatrix} x^{(t)} \\ h^{(t-1)} \\ c^{(t-1)} \end{bmatrix} \end{aligned} $$

LSTM’s Calculation

FeedForward

假设输入向量为 $\vec x \in R^n$, 隐变量$\vec h \in R^d$, 则$(1.5)$中, $W_* \in R^{d \times n}$, $U_* \in R^{d \times d}$, $W \in R^{4d \times (n+d)}$

$$ \begin{bmatrix} {\hat c_r}^{(t)} \\ {\hat g_i} \\ {\hat g_f} \\ {\hat g_o} \end{bmatrix} = \begin{bmatrix} W_c & U_c \\ W_i & U_i \\ W_f & U_f \\ W_o & U_o \end{bmatrix} \cdot \begin{bmatrix} x^{(t)} \\ h^{(t-1)} \end{bmatrix} = W \cdot I^{(t)} \tag{2.1} $$

$$ \begin{bmatrix} {\hat c}^{(t)} \\ g_i \\ g_f \\ g_o \end{bmatrix} = \begin{bmatrix} tanh({\hat c}_r^{(t)}) \\ sigmoid(\hat g_i) \\ sigmoid(\hat g_f) \\ sigmoid(\hat g_o) \end{bmatrix} \tag{2.2} $$

$$ c^{(t)} = g_{f} \otimes c^{(t-1)} + g_i \otimes {\hat c}^{(t)} \tag{2.3} $$

$$ h^{(t)} = g_o \otimes tanh(c^{(t)}) \tag{2.4} $$

Backward Propagation

以下$\delta x$皆代表$\frac{\partial L}{\partial x}$, 其中$L(y, \hat y)$为损失函数

由$(2.4)$, 给定$\delta h^{(t)}$, 求$\delta g_o$ , $\delta c^{(t)}$ $$ \begin{aligned} \delta g_o &= \frac{\partial h^{(t)}}{\partial g_o} \delta h^{(t)} \\ &= tanh(c^{(t)}) \otimes \delta h^{(t)} \end{aligned} \tag{2.5} $$ $$ \begin{aligned} \delta c^{(t)} &= \frac{\partial h^{(t)}}{\partial tanh(c^{(t)})} \frac{\partial tanh(c^{(t)})}{\partial c^{(t)}} \delta h^{(t)} \\ &= g_o \otimes (1 - tanh^2(c^{(t)})) \otimes \delta h^{(t)} \end{aligned} \tag{2.6} $$
由$(2.3)$, 给定$\delta c^{(t)}$, 求$\delta g_{f}$, $\delta c^{(t-1)}$, $\delta g_i$, $\delta {\hat c}^{(t)}$ $$ \begin{aligned} \delta g_i &= {\hat c}^{(t)} \otimes \delta c^{(t)} \\ \delta g_f &= c^{(t-1)} \otimes \delta c^{(t)} \\ \delta {\hat c}^{(t)} &= g_i \otimes \delta c^{(t)} \\ \delta c^{(t-1)} &= g_f \otimes \delta c^{(t)} \\ \end{aligned} \tag{2.7} $$
由$(2.2)$, 给定$\delta {\hat c}^{(t)}$, $\delta g_i$, $\delta g_{f}$, $\delta g_o$, 求$\delta {\hat c}_r^{(t)}$, $\delta \hat g_i$, $\delta \hat g_f$, $\delta \hat g_o$ $$ \begin{aligned} \delta \hat g_i &=g_i(1 - g_i) \otimes \delta g_i \\ \delta \hat g_f &=g_f(1 - g_f) \otimes \delta g_f \\ \delta \hat g_o &=g_o(1 - g_o) \otimes \delta g_o \\ \delta {\hat c}_r^{(t)} &= (1 - tanh^2({\hat c}^{(t)})) \otimes \delta {\hat c}^{(t)} \end{aligned} \tag{2.8} $$
由$(2.1)$, 给定$\delta {\hat c}_r^{(t)}$, $\delta \hat g_i$, $\delta \hat g_f$, $\delta \hat g_o$, 求$\delta W^{(t)}$, $\delta h^{(t-1)}$ $$ \delta W^{(t)} = \delta z^{(t)} \cdot (I^{(t)})^T \\ \delta I^{(t)} = W^T \cdot \delta z^{(t)} \\ $$
假设一共有$t$个时间步, 前向传播完毕之后更新权重 $$ \begin{aligned} \delta W &= \sum_{t=1}^{T}\delta W^{(t)} \\ W &= W - \epsilon \cdot \delta W \end{aligned} \tag{2.9} $$

有了Auto Grad, 我想大部分情况下你都不需要手推LSTM的BP…

GRU

贫穷限制了我们的计算能力

简而言之LSTM需要传递长短两条状态, 而GRU(Gate Recurrent Unit)只需要一个状态, 但性能和LSTM相似, 且需要更少的参数, 只需要三组系数(两个门和一个状态). 该结构是Chung, Junyoung, et al. (2014)的工作

Reset & Update Gate

GRU有两个门: Reset门$g_r$和Update门$g_z$, 由当前输入$x^{(t)}$和前一步输出$h^{(t-1)}$决定 $$ \begin{aligned} \begin{bmatrix} \hat g_r \\ \hat g_z \end{bmatrix} &= \begin{bmatrix} W_r & U_r \\ W_z & U_z \end{bmatrix} \cdot \begin{bmatrix} x^{(t)} \\ h^{(t-1)} \end{bmatrix} \\ \begin{bmatrix} g_r \\ g_z \end{bmatrix} &= \begin{bmatrix} \sigma(g_r) \\ \sigma(g_z) \end{bmatrix} \end{aligned} \tag{3.1} $$

Remember & Forget in One Shot

GRU的信息传递也涉及两步 $$ h’ = tanh(\begin{bmatrix} W_h & U_h\end{bmatrix} \cdot \begin{bmatrix} x^{(t)} \\ g_r \otimes h^{(t-1)} \end{bmatrix}) \tag{3.2} $$

$$ h^{(t)} = g_z \otimes h^{(t-1)} + (1 - g_z) \otimes h' \tag{3.3} $$ 其中$(3.2)$步涉及到选择性地添加将上一步的隐状态$h^{(t-1)}$和输入$x^{(t)}$, $(3.3)$步涉及到同时进行遗忘$(g_z \otimes h^{(t-1)})$和记忆$((1 - g_z) \otimes h’)$, 而遗忘和记忆都通过$g_z$进行, 且归一化为1

Pytorch implementation

Model

这里实现了一个LSTMTagger, 参考Sequence Models and Long-Short Term Memory Networks

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


import torch
from torch.autograd import Variable
import torch.nn as nn


class LSTMTagger(nn.Module):
    # 初始化隐藏层, 有两组状态, 即h和c
    def init_hidden(self):
        return (Variable(torch.zeros(1, 1, self.hidden_dim)),
                Variable(torch.zeros(1, 1, self.hidden_dim)))

    def __init__(self, num_embed, embed_dim, hidden_dim, num_label):
        super(LSTMTagger, self).__init__()
        self.hidden_dim = hidden_dim
        # 先将单词embed为embed_dim维向量
        self.embed = nn.Embedding(num_embed, embed_dim)
        # 再通过LSTM
        self.lstm = nn.LSTM(embed_dim, hidden_dim)
        # 每个输出通过一个线性+激活层输出为num_label维概率分布
        self.hidden2tag = nn.Linear(hidden_dim, num_label)
        self.log_softmax = nn.LogSoftmax()

        self.hidden = self.init_hidden()

    def forward(self, sentence):
        # 为每一句输入初始化h和c
        self.hidden = self.init_hidden()
        # word embedding
        embeds = self.embed(sentence)
        # 这里的out就是每一步输出的hidden state, 而self.hidden是最后一步的输出, 即out[-1] == self.hidden
        out, self.hidden = self.lstm(embeds.view(len(sentence), 1, -1), self.hidden)
        tag_scores = self.hidden2tag(out.view(len(sentence), -1))
        log_prob = self.log_softmax(tag_scores)
        return log_prob

Batch

Mini Batch Training train.shape == (n_batch, batch_size, embedding_dim) 假设一篇文档长为10000个单词, 输出标记每个单词的词性, 即有10000个输出. 设batch_size=50, 则式$(2.9)$中$T=50$, 每传播50个单位计算一次梯度并更新, 一共迭代n_batch=10000/50=200次, 每个单词被embed为embedding\_dim维, 计算细节如下(部分伪代码, 不是python):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


outputs = np.zeros((200,  50, 1))
for i\_batch from 1 to 200:
   # feedforward
   for step from 1 to 50:
       hidden, outputs[i_batch][step] = lstm(hidden, train[i_batch][step])
   loss = loss_function(outputs[i_batch], labels[i_batch])
   loss.backward()  # backprop
   # accumulate gradient
   grad = 0
   for step from 1 to 50:
       dW = W[step].grad()  # pytorch accumulate gradient automatically along timesteps
       grad += dW[i_ts]
   W = W - learning_rate * grad

Variable Length Training: Using pack_padded_sequence() 假设训练集为3句话, 分别包括(3, 2, 4)个单词, 每个单词进行2维 embedding, 原则上需要一句话一个batch进行训练, 但每句话长度不一样, 无法固定batch_size:

1
2
3
4
5


train = [
   [[1, 2], [3, 4], [5, 6]],
   [[7, 8], [9, 10]],
   [[4, 3], [6, 5], [2, 1], [0, 0]]
]

此时可以使用padding对齐所有变长的句子, 参考pytorch论坛的讨论

Appendix

Gradient of Activate Funtions

$$ \begin{aligned} y &= sigmoid(x) = \frac{1}{1 + e^x} \\ y’ &= y (1 - y) \end{aligned} \tag{a.1} $$

$$ \begin{aligned} y &= tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \\ y’ &= 1 - y^2 \end{aligned} \tag{a.2} $$

Reference

to be continued…