Logistic Regression, Softmax与最大熵

xiaoxuan

2017-03-27 1199 words 3 minutes

Contents

Logistic Regression的小结

第一部分 Logistic Regression

1. 线性回归的缺点

线性回归不适用于分类问题:

容易过拟合
$h_\theta$ can be >1 or <0

2. Logisitc Regression

2.1 模型假设

Sigmoid函数: $$h_\theta (x) = \frac {1}{1 + e^{-\theta^T x}}$$
概率学解释: 给定$\theta^T x$之后$y=1$的概率. 可以和SVM中的几何间隔类比一下. $\theta^T x$接近于正无穷的时候概率值接近1
此外, 既然是概率分布, 显然$P(y=0|x=\theta) + P(y=1|x=\theta) = 1$

2.2 似然函数

使用极大似然法估计模型参数, 对于每一个$(x^{(i)}, y^{(i)})$, 似然函数为: $$ [h_\theta (x^{(i)})]^{y^{(i)}} [1-h_\theta (x^{(i)})]^{1-y^{(i)}}$$ 对于整个训练集, 似然函数为 $$ \prod\limits_{i = 1}^n [h_\theta (x^{(i)})]^{y^{(i)}} [1-h_\theta (x^{(i)})]^{1-y^{(i)}}$$

似然函数很直观, 若$y=1$, 那么$h_\theta (x)$越接近1, 似然函数越大, 反之亦然.

2.3 损失函数

最大化似然函数就是最小化损失函数. 对似然函数取负就转化为损失函数了. 为了简化计算, 取log将似然函数的连乘转换为求和的形式. $$-Cost(h_\theta (x), y) = y log(h_\theta (x)) + (1 - y)log(1 - h_\theta (x))$$ 连乘转化为求和,就得到了总的损失函数 $$ J(\theta) = -\frac{1}{n}\sum\limits_{i=1}^{n}[y^{(i)}\log h_\theta(x^{(i)}) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] $$

3. 最优化算法

3.1 使用梯度下降最优化 $J(\theta)$

$$\frac{\partial}{\partial \theta_j} J(\theta) = \frac{1}{n}\sum\limits_{i=1}^{n}[(h_\theta (x^{(i)}) - y^{(i)})x_j^{(i)}]$$ $$\theta_j := \theta_j - \alpha \frac{1}{n} \sum\limits_{i=1}^{n}[(h_\theta (x^{(i)}) - y^{(i)})x_j^{(i)}]$$ 其中$\alpha$为学习率, 也就是每一步梯度下降的步长

3.2 其他最优化方法

梯度下降之外的其他优化方法 (不需要手动调参 $\alpha$):
- Conjugate descent
- IIS
- 拟牛顿法
- BGFS
- L-BFGS

3.3 多类别分类: One-vs-all

对于y,有超过0和1两个值的, 对每一个值做LR回归 ,然后输出每个模型的概率, 取最大的那个

4. Softmax

ufldl的参考资料

4.1 模型假设

logistic regression中的sigmoid函数可以写成: $$h_\theta (x) = \frac {e^{\theta^T x}}{1 + e^{\theta^T x}}$$ 如果$y_i$不是二元变量, 而是$K$元变量(例如$y \in \lbrace 1, 2, 3, \cdots, K \rbrace$), 自然推广到了softmax回归: $$ h_\theta (x) = \frac{1}{\sum\limits_{i = 1}^{K} e^{\theta_i^T x}} \begin{bmatrix}e^{\theta_1^T x}\\e^{\theta_2^T x}\\ \vdots \\ e^{\theta_K^T x} \end{bmatrix} $$ 其中 $$ \theta = \begin{bmatrix} \theta_1^T \\ \theta_2^T \\ \vdots \\ \theta_K^T \end{bmatrix}, \frac{ e^{\theta_j^T x^{(i)}}}{\sum\limits_{l = 1}^{K} e^{\theta_l^T x^{(i)}}} = P(y^{(i)}=j |x^{(i)}, \theta ) $$ 也就是softmax针对每一个可能的输出值都估计了一个概率值

4.2 损失函数

$$ J(\theta) = -\frac{1}{n} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{K} I(y^{(i)} = j) log \frac{ e^{\theta_j^T x^{(i)}}}{\sum\limits_{l = 1}^{K} e^{\theta_l^T x^{(i)}}} $$

简单解释: 内层循环把输出和$y^{(i)}$符合的值全部统计到了损失函数中, 他们构成了让损失函数降低的要素(其他值都是0), 外层累加了所有samples

4.3 参数冗余

实际上对$\theta$的每一行加上同一个向量之后输出值不会改变, 因此参数是可以压缩的. 而其Hessian 矩阵是奇异的/不可逆的, 因此使用牛顿法会优化会遇到困难, 虽然$J(\theta)$是凸的

4.4 正则化

加入L2正则项之后顺带解决了Hessian 矩阵不可逆的问题 $$ J(\theta) = -\frac{1}{n} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{K} I(y^{(i)} = j) log \frac{ e^{\theta_j^T x^{(i)}}}{\sum\limits_{l = 1}^{K} e^{\theta_l^T x^{(i)}}} + \frac{\lambda}{2} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{K} \theta_{ij}^2 $$

梯度是 $$ \nabla_{\theta_j} J(\theta) = -\frac{1}{n} \sum\limits_{i=1}^{n} x^{(i)}(I(y^{(i)} = j) - P(y^{(i)}=j |x^{(i)}, \theta )) $$ 这是一个$n$维向量, 和$x$规格一致, 第$i$个元素代表了$\frac{\partial J(\theta)}{\partial \theta_{ji}}$, 即$J(\theta)$对$\theta_j$第$i$个分量的偏导数.

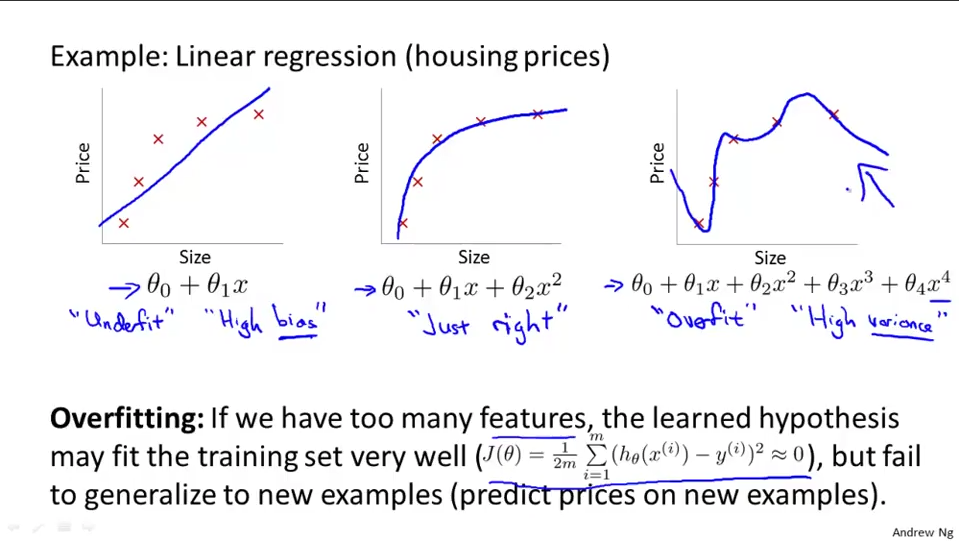
5. 正则化(Regularzation)

过拟合的问题(看图吧)

处理过拟合问题

降低特征维度 (manually/model selection)
正则化: add panalize terms to some less important parameters, or panalize all the parameters(except for $\theta_0$)

Regularized Linear Regression $$\displaystyle \theta_j := \theta_j(1-\alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j$$

For normal equation, regularization would also make $X^T X$ invertible

Regularized Logistic Regression

Literally the same as Regularized Linear Regression except for the form of $h_\theta (x)$

第二部分最大熵模型

施工中