支持向量机(SVM)

2017-03-24 2165 words 5 minutes

Contents

旧文章的翻译, 主要参考自李航的统计学习方法一书.

第一部分基本概念

1.1 超平面(Hyperplane)

考虑一个二分类问题: $$\text{Training set: } T = \left \lbrace (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}) …(x^{(N)}, y^{(N)}) \right \rbrace \\ \text{in which }x^{(i)} \in R^n, y^{(i)} \in \lbrace +1, -1 \rbrace, i=1,2…N$$

假设样本空间线性可分, 则有超平面: $$ w \cdot x + b = 0 \text{, in which }w, b \in R^N$$

1.2 间隔(Margin)

在希尔伯特空间中, 点到平面的距离是: $$ \gamma^{(i)} = \left \vert \frac{w}{\Vert w \Vert} \cdot x^{(i)} + \frac{b}{\Vert w \Vert} \right \vert \tag{1.1}$$
为了去掉绝对值, 令在超平面法向量一侧的$x^{(i)}$标记为+1, 另一侧的标记为-1, $\gamma^{(i)}$ 可以被定义为: $$ \gamma^{(i)} = y^{(i)} \left ( \frac{w}{\Vert w \Vert} \cdot x^{(i)} + \frac{b}{\Vert w \Vert} \right ) \tag{1.2}$$

1.3 寻找更好的分隔

预测函数 (Predicting function)
换句话说如果我们已经找到了超平面 $ w^{*} \cdot x + b^{*} = 0 $, 给定一个样本点 $x^{(i)}$, 预测函数是: $$y^{(i)} = f(x^{(i)}) = sign(w^{*} \cdot x^{(i)} + b^{*}) \tag{1.3}$$
几何间隔 (Geometric margin)
几何间隔就是点到平面的最大距离: $$ \gamma = \min \limits_{i = 1,2…N} \quad \gamma^{(i)} \tag{1.4}$$
函数间隔 (Functional margin)
函数间隔被定义为: $$ \hat \gamma^{(i)} = y^{(i)} \left ( w \cdot x^{(i)} + {b} \right ) = {\Vert w \Vert} \gamma^{(i)} \tag{1.5}$$ 函数间隔可以被考虑为分类的置信度, 可以被用来简化运算

1.4 硬间隔最大化: 找到最大间隔是SVM的目标

$$ \begin{align} & \max \limits_{w,b} \quad \gamma \\ & s.t. \quad y^{(i)} \left ( \frac{w}{\Vert w \Vert} \cdot x^{(i)} + \frac{b}{\Vert w \Vert} \right ) \ge \gamma , \quad i=1,2,…,N \tag{1.6} \end{align}$$

使用函数间隔, 原问题可以被定义为: $$ \begin{align} & \max \limits_{w,b} \quad \frac{\hat \gamma}{\Vert w \Vert} \\ & s.t. \quad y^{(i)} \left ( w \cdot x^{(i)} + {b} \right ) \ge \hat \gamma , \quad i=1,2,…,N \end{align} \tag{1.7}$$

给定一个超平面, $\Vert w \Vert$ 和 $\Vert b \Vert$ 是可变的: $w$ 和 $b$ 只要保持比例相同,则超平面不变. 为了限制这两个变量,令 $\hat\gamma = 1$(这样就可以让 $\Vert w \Vert$ 保持不变), 问题最终被定义为: $$ \begin{align} & \min \limits_{w,b} \quad \frac{1}{2} {\Vert w \Vert}^2 \\ & s.t. \quad y^{(i)} \left ( w \cdot x^{(i)} + {b} \right ) - 1 \ge 0, \quad i=1,2,…,N \end{align} \tag{1.8}$$

$\min \limits_{w,b} \frac{1}{2} {\Vert w \Vert}^2$ 和原始问题 $ \max \limits_{w,b} \frac{1}{\Vert w \Vert} $ 是等价的.

1.6 软间隔最大化

如果样本空间线性不可分, 为每个样本设置一个松弛变量 $\xi \in R^n$ 那么 (1.8) 成为: $$ y^{(i)} \left ( w \cdot x^{(i)} + {b} \right ) + \xi_i - 1 \ge 0 \tag{1.9}$$ 对每个样本支付代价 $\xi_i$ 目标函数变为: $$ \frac{1}{2} {\Vert w \Vert}^2 + C \sum\limits_{i=1}^{N}\xi_i \tag{1.10}$$ $C$ 称为惩罚参数, 更大的$C$ 意味着对误分类的样本惩罚更大

1.7 Support Vector (支持向量)

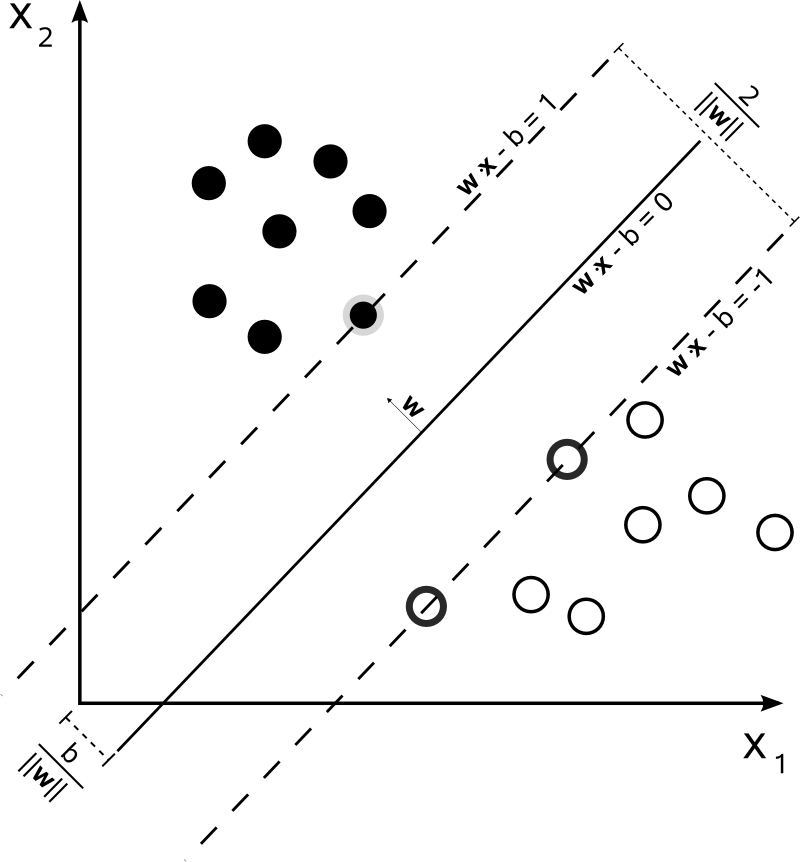顾名思义, 支持向量是"支持"超平面的向量

第二部分: 解决硬间隔最大化问题

2.1 解决硬间隔最大化问题

(1.8) 是个凸二次规划问题使用拉格朗日乘子法, (1.8) 可以表示为: $$ L(w,b,\alpha) = \frac{1}{2} {\Vert w \Vert}^2 + \sum\limits_{i=1}^{N} \alpha_i (1-y^{(i)}(w \cdot x^{(i)} + b)), \alpha_i \ge 0 \tag{2.1}$$

他的对偶问题是: $$\max\limits_{\alpha} \ \min\limits_{w,b} L(w,b,\alpha) \tag{2.2}$$

2.2 求解 $\min\limits_{w,b} L(w,b,\alpha)$

$$ \nabla_w L(w,b,\alpha) = w - \sum\limits_{i=1}^{N} \alpha_i y^{(i)} x^{(i)} = 0 \\ \nabla_b L(w,b,\alpha) = \sum\limits_{i=1}^{N} \alpha_i y^{(i)} = 0 \tag{2.3}$$

组合(2.3) 和 (2.1), 得到如下对偶问题: $$ \begin{align} & \max\limits_{\alpha} \left\lbrace - \frac{1}{2} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} \alpha_i \alpha_j y^{(i)} y^{(j)} (x^{(i)} \cdot x^{(j)}) + \sum\limits_{i=1}^{N} \alpha_i \right\rbrace \\
& s.t. \quad \sum\limits_{i=1}^{N} \alpha_i y^{(i)} = 0, \alpha_i \ge 0 \end{align} \tag{2.4}$$

2.3 求解 $\alpha$

$$ \begin{align} & \min\limits_{\alpha} \left\lbrace \frac{1}{2} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} \alpha_i \alpha_j y^{(i)} y^{(j)} (x^{(i)} \cdot x^{(j)}) - \sum\limits_{i=1}^{N} \alpha_i \right\rbrace \\
& s.t. \quad \sum\limits_{i=1}^{N} \alpha_i y^{(i)} = 0, \alpha_i \ge 0 \end{align} \tag{2.5}$$

$\alpha^{*}$ 需要满足KKT条件 (2.3), (2.4) 和 $ \alpha_i^{*} (1-y^{(i)}(w^{*} \cdot x^{(i)} + b^{*})) = 0 $

2.4 求解 $w,b$

一旦 $\alpha^{*}$ 已经求解出, 那么: $$ w^{*} = \sum\limits_{i=1}^{N} \alpha_i^{*} y^{(i)} x^{(i)} \\ b^{*} = y^{(j)} - \sum\limits_{i=1}^{N} \alpha_i^{*} y^{(i)} (x^{(i)} \cdot x^{(j)}) \tag{2.6}$$ 其中$(x^{(j)}, y^{(j)})$ 满足: $ 1-y^{(j)}(w^{*} \cdot x^{(j)} + b^{*}) = 0 $, 这意味着该点是支持向量

注意到当 $\alpha_i = 0$, $(x^{(i)}, y^{(i)})$ 对 $w$ 和 $b$ 没有任何贡献, 这就意味着只有少数满足$\alpha_i > 0$, 即 $ 1-y^{(i)}(w^{*} \cdot x^{(i)} + b^{*}) = 0 $ 的支持向量决定了超平面.

第三部分: 解决软间隔最大化问题

3.1 求解 $\min\limits_{w,b} L(w,b,\xi,\alpha,\mu)$

二次凸优化问题是: $$ \begin{align} & \min\limits_{w, \xi} \quad \frac{1}{2} {\Vert w \Vert}^2 + C \sum\limits_{i=1}^{N}\xi_i \\ s.t. \quad & y^{(i)} \left ( w \cdot x^{(i)} + {b} \right ) + \xi_i - 1\ge 0 \ & \xi_i \ge 0\tag{1.10} \end{align}$$ 对(1.10)使用拉格朗日乘子法, (1.10) 可以被表示为:

$$ \begin{align} & L(w,b,\xi,\alpha,\mu) = \frac{1}{2} {\Vert w \Vert}^2 + C \sum\limits_{i=1}^{N}\xi_i + \sum\limits_{i=1}^{N} \alpha_i (1 -\xi_i - y^{(i)}(w \cdot x^{(i)} + b)) + \sum\limits_{i=1}^{N} \mu_i(-\xi_i) \tag{3.1} \end{align}$$

$$ \nabla_w L(w,b,\xi,\alpha,\mu) = w - \sum\limits_{i=1}^{N} \alpha_i y^{(i)} x^{(i)} = 0 \\ \nabla_b L(w,b,\xi,\alpha,\mu) = \sum\limits_{i=1}^{N} \alpha_i y^{(i)} = 0 \\ \nabla_{\xi_i} L(w,b,\xi,\alpha,\mu) = C-\alpha_i - \mu_i = 0 \tag{3.2}$$

幸运的是他们和 (2.4) 以及 (2.5) 有相同的形式

3.2 求解 $\alpha$

软间隔最大化的对偶问题是:

$ \begin{align} & \min\limits_{\alpha} \quad \frac{1}{2} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} \alpha_i \alpha_j y^{(i)} y^{(j)} (x^{(i)} \cdot x^{(j)}) - \sum\limits_{i=1}^{N} \alpha_i \end{align} \tag{3.2}$

$ s.t. \quad \sum\limits_{i=1}^{N} \alpha_i y^{(i)} = 0, \quad \alpha_i \ge 0, \quad \mu_i \ge 0, \quad C- \alpha_i-\mu_i =0 \tag{3.3} $

(3.3) 可以被简化为:

$$ s.t. \quad \sum\limits_{i=1}^{N} \alpha_i y^{(i)} = 0, \quad 0 \le \alpha_i \le C \tag{3.4}$$

3.3 求解 $w,b$

一旦 $\alpha^{*}$ 被求解, 有: $$ w^{*} = \sum\limits_{i=1}^{N} \alpha_i^{*} y^{(i)} x^{(i)} \\ b^{*} = y^{(j)} - \sum\limits_{i=1}^{N} \alpha_i^{*} y^{(i)} (x^{(i)} \cdot x^{(j)}) \tag{3.5}$$ 其中$(x^{(j)}, y^{(j)})$ 满足: $ 0 \le \alpha_j \le C $, 亦即 $ 1 - \xi_i -y^{(j)}(w^{*} \cdot x^{(j)} + b^{*})) = 0 $, 意味着这些向量满足在分类边界的区间之内.

3.4 SVM的损失函数: 合页损失函数(Hinge loss function)

令 $\quad [ 1 - y^{(i)} \left ( w \cdot x^{(i)} + {b} \right ) ]_+ = \xi_i $, (1.10) 可以被表达为

$$\min\limits_{w,b} \quad \sum\limits_{i=1}^N \xi_i + \lambda {\Vert w \Vert}^2 \tag{3.6}$$

令 $\lambda = \frac{1}{2C}$, 和 (1.10) 是等价的, 那么损失函数可以被表示为:

$$ \sum\limits_{i=1}^N[ 1 - y^{(i)} \left ( w \cdot x^{(i)} + {b} \right ) ]_+ + \lambda {\Vert w \Vert}^2 \tag{3.7}$$

称合页损失函数

第四部分: 序列最小最优化算法

4.1 问题描述

优化问题是: $ \begin{align} & \min\limits_{\alpha} \quad \frac{1}{2} \sum\limits_{i=1}^{N} \sum\limits_{j=1}^{N} \alpha_i \alpha_j y^{(i)} y^{(j)} K(x^{(i)}, x^{(j)}) - \sum\limits_{i=1}^{N} \alpha_i \end{align} \tag{3.2}$

$ s.t. \quad \sum\limits_{i=1}^{N} \alpha_i y^{(i)} = 0, \quad 0 \le \alpha_i \le C \tag{3.4}$

为了高效地解决这个优化问题, 引入序列最小最优化算法(Sequantial Minimal Optimization)

4.2 序列化求解凸二次规划问题

假设在所有 $\alpha_i$ 中, 只把 $\alpha_1, \alpha_2$ 当成变量, 所有其他 $\alpha_i(i \neq 1, 2)$ 都是常量, $\alpha_2^{i}$ 是第 $\alpha_2$ 的第$i$次迭代结果, 为了表示方便首先定义一些变量:

$$ L = \begin{cases} max\lbrace 0, \alpha_2^i - \alpha_1^i \rbrace, & y^{(1)} \neq y^{(2)} \\ max\lbrace 0, \alpha_2^i + \alpha_1^i - C \rbrace, & y^{(1)} = y^{(2)} \end{cases} $$

$$ H = \begin{cases} min \lbrace C, \alpha_2^i - \alpha_1^i + C \rbrace, & y^{(1)} \neq y^{(2)} \\ min \lbrace C, \alpha_2^i + \alpha_1^i \rbrace, & y^{(1)} = y^{(2)} \end{cases} $$

$$E_i = g(x^{(i)}) - y^{(i)} = \left( \sum\limits_{j=1}^{N} \alpha_j y^{(j)} K(x^{(i)}, x^{(j)})+b \right)- y^{(i)} \tag{SMO.1}$$

那么利用 $H$ 和 $L$ 去约束 $\alpha_2$, 在第 $(i+1)$ 次迭代中:

$$ \alpha_2^{i+1, unc} = \alpha_2^{i} + \frac { y^{(2)}(E_1 - E_2)}{K_{11}+K_{22}-2K_{12}} \tag{SMO.2}$$

$$ \alpha_2^{i+1} = \begin{cases} H, & \alpha_2^{i+1, unc} > H \\ \alpha_2^{i+1, unc}, & L \le \alpha_2^{i+1, unc} \le H \\ L, & \alpha_2^{i+1, unc} < L \end{cases} \tag{SMO.3} $$

$$ \alpha_1^{i+1} = \alpha_1^{i} + y^{(1)}y^{(2)}(\alpha_2^{i} - \alpha_2^{i+1}) \tag{SMO.4} $$

4.3 启发式选择 $\alpha_1, \alpha_2$

对每个 $\alpha_i$, KKT约束是: $$ \begin{align} \alpha_i = 0 \quad & \Leftrightarrow \quad y^{(i)} g(x^{(i)}) \ge 1 \quad \text{(Out of the border)} \\ 0 < \alpha_i < C \quad & \Leftrightarrow \quad y^{(i)} g(x^{(i)}) = 1 \quad \text{(On the border)} \\ \alpha_i = C \quad & \Leftrightarrow \quad y^{(i)} g(x^{(i)}) \le 1 \quad \text{(Inside the border)} \end{align} \tag{SMO.5} $$

选择 $\alpha_1$:

遍历所有满足$0 < \alpha_i < C$的点, 检查他们是否满足KKT条件, 若满足则再遍历整个训练集

选择 $\alpha_2$:

寻找一个样本 $(x^{(i)}, y^{(i)})$ 使得 $\vert E^i_1 - E^i_2 \vert$ 有最大的变动. 为了节省运算量, 提前缓存 $E_i$

4.4 计算新的 $b$ 和 $E_i$

计算 $b$ $$ b_1^{i+1} = b^i -[E_1^i + y^{(1)}K_{11}(\alpha_1^{i+1} - \alpha_1^{i}) + y^{(2)}K_{21}(\alpha_2^{i+1} - \alpha_2^{i}) ] \\ b_2^{i+1} = b^i -[E_2^i + y^{(1)}K_{12}(\alpha_1^{i+1} - \alpha_1^{i}) + y^{(2)}K_{22}(\alpha_2^{i+1} - \alpha_2^{i}) ] \tag{SMO.6} $$

$$b^{i+1} = \begin{cases} b_{1}^{i+1} = b_{2}^{i+1}, & 0 < \alpha_1^{i+1}, \alpha_2^{i+1} < C \\ \frac {1}{2} (b_{1}^{i+1} + b_{2}^{i+1}), & \alpha_1^{i+1}, \alpha_2^{i+1} = 0 ; or ; C \end{cases} $$ 2. Calculate $E_i$ using $\alpha_1^{i+1}, \alpha_2^{i+1}, b^{i+1}$ $$ E_i = \sum\limits_{j \in S} \alpha_j y^{(j)} K(x^{(i)}, x^{(j)})+b^{i+1} - y^{(i)} $$

第五部分: 核函数方法

施工中