Laniakea
文章 练习场 码农 Tags
Laniakea

Contents

Adaboost算法 + python实现

   3766 words   8 minutes 

Adaboost的总结

第一部分: AdaBoost简介

1.1 强可学习和弱可学习

  1. 在概率近似正确(PAC)学习框架中, 一个类如果存在:
    • 一个多项式复杂度的学习算法,正确率略大于随机猜测(例如二分类问题中大于1/2),称弱可学习的类
    • 一个多项式复杂度的学习算法,并且正确率很高,称强可学习的类
  2. Kearns和Valiant证明了强可学习和弱可学习是等价的
  3. Adaboost算法就是将弱学习器组成强学习器的算法

1.2 组合弱分类器

  1. 测试集: $$T = \left\lbrace (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \cdots, (x^{(N)}, y^{(N)})\right\rbrace, \quad x \in \chi \subseteq R^N, y \in \lbrace +1, -1 \rbrace \\ \text{with weights: } D_i = (w_{i1}, w_{i2}, \cdots, w_{iN})$$

  2. 分类器 $$G_m(x): \chi \to \lbrace +1, -1\rbrace, \quad G(x) = \sum\limits^M_{i=1} \alpha_m G_m(x) \\ \text{with weights: } A = (\alpha_{1}, \alpha_{2}, \cdots, \alpha_{M}) $$

1.3 AdaBoost 算法

输入: 训练集 $T$, m个弱分类器 $G_m(x)$ 输出: 集成分类器 $G(x)$

  1. 初始化权重: $$ D_1 = (w_{11}, w_{12}, \cdots, w_{1N}), \quad w_{1i} = \frac{1}{N} $$

  2. For $m = 1,2, \cdots, M$:
    (a) 对具有权重分布 $D_m = (w_{m1}, w_{m2}, \cdots, w_{mN})$ 的训练集 $T$ 训练出弱分类器 $G_m(x)$
    (b) 计算弱分类器 $G_m(x)$ 在 $T$ 上的误差率: $$ e_m = P(G_m(x^{(i)}) \neq y^{(i)}) = \sum\limits^N_{i=1} w_{mi}I(G_m(x^{(i)}) \neq y^{(i)}) \tag{1}$$
    (c) 计算 $G_m(x)$ 的系数 $\alpha_m$: $$ \alpha_m = \frac{1}{2} ln \frac{1-e_m}{e_m} \tag{2}$$
    (d) 更新训练集的权重分布 $D_{m+1}$:
    $$ D_{m+1} = (w_{m+1, 1}, w_{m+1, 2}, \cdots, w_{m+1, N}) $$ $$w_{m+1, i} =\begin{cases} \frac{w_{mi}}{Z_m} e^{-\alpha_m}, & G_m(x^{(i)}) = y^{(i)} \\ \\ \frac{w_{mi}}{Z_m}e^{\alpha_m}, & G_m(x^{(i)}) \neq y^{(i)} \end{cases} = \frac {w_{mi}e^{-\alpha_m y^{(i)} G_m(x^{(i)})}} {Z_m} \tag{3}$$ $$Z_m = \sum\limits^N_{i=1}w_{mi}e^{-\alpha_m y^{(i)} G_m(x^{(i)})} $$ 这里 $Z_m$ 是规范化因子, 使得 $D_{m+1}$ 成为一个概率分布, 保证了 $\sum\limits^N_{i=1}w_{m+1, i} = 1$

最后,组合所有弱分类器 $G_m(x)$: $$ f(x) = \sum\limits^M_{i=1} \alpha_m G_m(x), \quad G(x) = sign(f(x))$$

1.4 实现细节

注意到每次迭代测试集中的样本都具有不同的权重, 实现方法有:

  1. 在每个弱分类器计算损失函数的时候, 对相应样本的loss乘以权重
    • 缺点: 需要修改弱分类器, 在loss中引入权重
  2. 不需要修改弱分类器的方案: 直接修改训练集
    • 每次迭代都使用 $D_i$ 作为概率分布从原始数据集中生成新的数据集进行训练

1.5 直观解释

https://my-imgshare.oss-cn-shenzhen.aliyuncs.com/Logistic.png

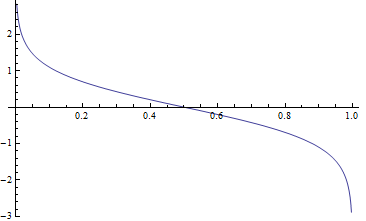
  • 对模型来说, 这里显示了弱分类器 $G_m(x)$的权重, $ \alpha_m = \frac{1}{2} ln \frac{1-e_m}{e_m} $ 与误差 $e_m$, 变化的关系. 显然更精确的弱分类器具有更大的权重
  • 相反, 对训练集数据来说, 从 (3) 可知被误分类的样本的权重会增加, 被正确分类的样本权重会降低, 增加/降低的速度都是指数级别的.

第二部分: Adaboost与前向分步算法

2.1 加法模型与前向分步算法

考虑一个与adaboost相似的累加模型 (additive model) : $$ f(x) = \sum\limits_{m=1}^M \beta_m b(x; \gamma_m) $$ in which $b(x; \gamma_m)$ 是基分类器, $\gamma_m$ 是基分类器的参数, $\beta_m$ 是基分类器的权重.

为了最小化损失函数, 提出前向分步算法(forward stagewise algorithm), 每一步只学习一个基函数及其系数, 即每一步中把其他所有模型看成常数, 只优化一个模型. 这是前向分步算法的核心概念.

2.2 前向分步算法

输入: 训练集 $T = \lbrace (x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \cdots, (x^{(N)}, y^{(N)}) \rbrace$, 损失函数$L(y, f(x))$, 基分类器 $b(x; \gamma)$
输出: 累加模型 $f(x)$, 初始化 $f_0(x) = 0$

  1. For $m = 1,2,\cdots,M$:
    • 最小化损失函数: $$ (\beta_m, \gamma_m) = arg\min\limits_{\beta, \gamma} \sum\limits_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + \beta b(x^{(i)};\gamma)) $$
    • 更新 $f(x)$: $$ f_m(x) = f_{m-1}(x) + \beta_m b(x^{(i)};\gamma_m)$$
  2. 生成累加模型: $$ f(x) = \sum\limits_{m=1}^M \beta_m b(x; \gamma_m) $$

2.3 Adaboost与前向分步算法

以下证明, adaboost算法实际上就是一个使用累加模型, 且损失函数为指数函数的前向分步算法

假设损失函数为指数损失函数(exponential loss function): $$ L(y, f(x)) = exp(-yf(x)) $$ 可以证明指数损失函数最小化, 则分类错误率也最小化, 说明指数损失函数是分类任务0/1损失函数的一致替代损失函数. 但它连续可微, 因此更适合优化.

在第$m$次迭代中: $$ f_m(x) = f_{m-1}(x) + \alpha_mG_m(x), \\ \text{其中 } f_{m-1}(x) = \sum\limits_{m=1}^{M-1} \alpha_mG_m(x) $$ 为了最小化 $$\begin{align} (\alpha_m, G_m) & = arg\min\limits_{\alpha, G} \sum\limits_{i=1}^N exp \left\lbrace -y^{(i)}(f_{m-1}(x^{(i)}) + \alpha_m G_m(x^{(i)}))\right\rbrace \\ & = arg\min\limits_{\alpha, G} \sum\limits_{i=1}^N w_{mi} exp \left\lbrace -y^{(i)} \alpha_m G_m(x^{(i)}) \right\rbrace \end{align} $$ 其中 $w_{mi} = exp(-y^{(i)} f_{m-1}(x^{(i)}))$, 则损失函数仅依赖于$\alpha$ 和 $G$.

为了证明算法中的$\alpha_m^*, G_m^*$ 与adaboost中的 $\alpha_m, G_m$ 等价:

  1. 对任意 $\alpha > 0$, 使损失函数最小的 $G_m^*(x)$ 由下式得到: $$ G_m^*(x) = arg\min\limits_{G} \sum\limits_{i=1}^N w_{mi} I(y^{(i)} \neq G(x^{(i)})) $$ 此分类器即为adaboost算法中的基分类器, 即 $G_m^*(x) = G_m(x)$
  2. 求 $\alpha_m$ $$\begin{align} L(\alpha, G_m) & = \sum\limits_{i=1}^N w_{mi} exp \left\lbrace -y^{(i)} \alpha G_m(x^{(i)}) \right\rbrace \\ & = (e^{\alpha} - e^{-\alpha}) \sum\limits_{\neq} w_{mi} + e^{-\alpha} \sum\limits w_{mi} \end{align} $$ 其中$\sum\limits_{\neq}$ 是$\sum\limits_{y^{(i)} \neq G(x^{(i)})}$的缩写, $\sum$ 是$\sum\limits_{i=1}^N$ 的缩写

对$\alpha$求导并使导数为0, 即得到使损失函数最小的$\alpha$ $$\frac {\partial L(\alpha, G_m)} {\partial \alpha} = (e^{\alpha} + e^{-\alpha}) \sum\limits_{\neq} w_{mi} - e^{-\alpha} \sum\limits w_{mi} = 0$$ s.t. $$(e^{\alpha} + e^{-\alpha}) \frac{\sum\limits_{\neq} w_{mi}}{\sum\limits w_{mi}} - e^{-\alpha} = 0$$ s.t. $$(e^{\alpha} + e^{-\alpha}) \epsilon_m - e^{-\alpha} = 0$$ s.t. $$ \alpha^* = \frac{1}{2}ln \frac{1-\epsilon_m}{\epsilon_m} $$ 其中 $\epsilon_m = \frac{\sum\limits_{\neq} w_{mi}}{\sum\limits w_{mi}}$, 即为 $G_m^*(x)$ 的损失函数 最后我们得到 $(\alpha_m, G_m)$ 是和adaboost中的一致的

第三部分: Code Review

项目源码见github

3.1 数据集介绍

Horse Colic Data Set

  • 马是否得了疝气的预测
  • 数据集大小: 68
  • 特征数目: 24
  • 数据集是否完整: 有缺失数据, 用0补全

3.2 项目结构

  1. 基分类器使用决策树桩
    • 基分类器的数据结构: 采用字典结构
    • 基分类器的训练: 损失函数为0-1损失函数, 找到最好阈值
  2. adaboost算法
    • 集成分类器的数据结构: 采用类保存权重list和基分类器list
    • 算法训练
  3. 保存/载入模型的功能: 读取/保存为json文件
  4. 模型评估: 准确率和ROC曲线

3.3 基分类器:决策树桩

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

    import numpy as np
    def stump_classifier(data_matrix, feature_index, threshold, rule='lt'):
        """
        :param: data_matrix: 测试集, 样本按行排列
        :param: feature_index: 用来分类的特征序号
        :param: threshold: 阈值
        :param: rule: 规则, 默认情况下是小于阈值被分类为-1.0
        决策树桩
        输入: 测试集
        输出: 预测结果(以1,-1标注)
        """
        results = np.ones((data_matrix.shape[0], 1))
        feature_values = data_matrix[:, feature_index]
        if rule == 'lt':
            results[np.where(feature_values <= threshold)[0]] = -1.0
        elif rule == 'gt':
            results[np.where(feature_values > threshold)[0]] = -1.0
        else:
            print('ERROR: rule not recognized, use default as lt.')
            results[np.where(feature_values <= threshold)[0]] = -1.0
        return results

3.4 基分类器训练过程: 寻找最小损失的阈值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

    import numpy as np
    def create_stump(data_matrix, labels, data_weights, step_number=10):
        """
        :param: data_matrix: 测试集, 样本按行排列
        :param: labels: 标注
        :param: data_weights: 训练集样本权重
        :param: step_number: 迭代次数, 亦即设置阈值每一步的步长
        :return: stump: 决策树桩, 用dict实现
        :return: return_prediction: 预测的标注值
        :return: min_error: 最小损失函数值
        决策树桩训练函数
        输入: 训练集, 训练集权重, 迭代次数
        输出: 决策树桩, 输出值, 最小损失
        """
        m, n = np.shape(data_matrix)
        stump = {}
        return_prediction = np.zeros((m, 1))
        min_error = np.inf
    
        # 遍历特征
        for i in range(n):
            min_value = data_matrix[:, i].min()
            max_value = data_matrix[:, i].max()
            step_size = (max_value - min_value) / float(step_number)
            # 按步长设定阈值
            for j in range(-1, step_number + 1):
                for rule in ['lt', 'gt']:
                    threshold = min_value + j * step_size
                    prediction = stump_classifier(data_matrix, i, threshold, rule)
                    # is_error用来存放是否错误的标记, 即I(prediction = labels)
                    is_error = np.ones((m, 1))
                    is_error[prediction == labels] = 0
                    # 损失乘以归一化的权重
                    weighted_error = np.dot(data_weights.T, is_error)
                    if weighted_error < min_error:
                        min_error = weighted_error
                        return_prediction = prediction.copy()
                        stump['feature_index'] = i
                        stump['threshold'] = threshold
                        stump['rule'] = rule
        return stump, return_prediction, min_error

3.5 集成分类器数据结构

1
2
3
4
5
6
7
8
9

    import numpy as np
    class Model:
        """
        :return: model_weights: np数组,弱分类器权重
        :return: model_list: weak model list, 其中每个弱分类器用dict实现
        """
        def __init__(self, size=10):
            self.model_weights = np.zeros((size, 1))
            self.model_list = []

3.6 Adaboost训练集成分类器

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

    import numpy as np
    def adaboost_train(data_matrix, labels, iteration=40):
        """
        :param: data_matrix: (m,n) np数组, 训练集, 样本按行排列
        :param: labels: (m,1) np数组 标注
        :param: iteration: int 弱分类器个数
        输入训练集和弱分类器个数, 输出模型
        """
        number = data_matrix.shape[0]
        data_weights = np.ones((number, 1)) / number        # 初始化训练集权重为1/number
        m = Model(iteration)                                # 初始化模型权重为0
        for i in range(iteration):
            stump, predictions, weighted_error = st.create_stump(data_matrix, labels, data_weights)
            m.model_list.append(stump)
            m.model_weights[i] = 0.5 * math.log((1.0 - weighted_error) / max(weighted_error, 1e-16))
            data_weights = data_weights * np.exp(-1.0 * m.model_weights[i] * labels * predictions)
            data_weights = data_weights / np.sum(data_weights)
        return m

3.7 集成分类器

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

    import numpy as np
    def adaboost_classify(input_matrix, m):
        """
        :param: data_matrix: (m,n) np数组,测试集, 样本按行排列
        :param: m: 模型
        :return: models_output: (m,1) np数组,强分类器输出值
        ensemble model, 输入训练集, 返回输出结果
        """
        models_output = np.zeros((input_matrix.shape[0], 1))
        for i in range(len(m.model_list)):
            model_prediction = st.stump_classifier(input_matrix,
                                                   m.model_list[i]['feature_index'],
                                                   m.model_list[i]['threshold'],
                                                   m.model_list[i]['rule'])
            models_output += m.model_weights[i] * model_prediction
        return models_output

3.8 分类器测试函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

    import numpy as np
    def adaboost_test(data_matrix, labels, m):
        """
        :param: data_matrix: 测试集, 样本按行排列
        :param: labels: 标注
        输入测试集和模型, 输出模型参数, 输出结果和正确率, 返回输出结果
        """
        models_output = adaboost_classify(data_matrix, m)
        i_vec = (np.sign(models_output) == labels).astype(int)
        error_rate = 1 - np.count_nonzero(i_vec) / float(data_matrix.shape[0])
    print 'model weights:'+'\n', m.model_weights, '\n'+'models_output:'+'\n', models_output, '\n'+'error     rate: ', error_rate
        return models_output

3.9 保存模型参数到json文件

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

    import json
    def save_model(m):
        weights_json = json.dumps(m.model_weights.tolist(), indent=4, separators=(',', ': '))
        models_json = json.dumps(m.model_list, indent=4, separators=(',', ': '))
        with open("model/model_weights.json", 'w') as fp:
            fp.write(weights_json)
        with open("model/model_list.json", 'w') as fp:
            fp.write(models_json)

    def load_model():
        with open("model/model_weights.json") as fp:
            weights_json = json.loads(fp.read())
            weights_list = np.array(weights_json)
            size = weights_list.shape[0]
            model = ab.Model(size)
            model.model_weights = weights_list
    
        with open("model/model_list.json") as fp:
            model_list = json.loads(fp.read())
            model.model_list = model_list
        return model

3.10 测试用例

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

    import numpy as np
    import adaboost as ab     # adaboost训练脚本
    import test_toolkit as tt # 测试用工具包, 主要用于数据预处理(未展示)
    import plot_roc as plot   # 绘制ROC曲线, 评估模型优劣(未展示)

    # 载入数据
    data_matrix = tt.load_data('test_data/horseColicTest2.txt')
    
    # 预处理, 测试集/训练集分为8:2
    train_matrix, cv_matrix, test_matrix = tt.split_data(data_matrix, (0.8, 0.0))
    train_matrix_x, class_vector = tt.separate_x_y(train_matrix)
    
    # ------------------1. 自己训练模型----------------------
    m = ab.adaboost_train(train_matrix_x, class_vector)
    
    # -----------------2. 载入预训练模型----------------------
    # m = load_model()
    
    # -------------------测试模型泛化能力---------------------
    test_matrix_x, test_labels = tt.separate_x_y(test_matrix)
    results = ab.adaboost_test(test_matrix_x, test_labels, m)
    
    # 绘制ROC曲线
    plot.plot_roc(results, test_labels)
    
    # 保存模型
    save_model(m)

3.11 训练结果

1
2
3
4
5

    models_output:
    [[ 1. -1.  1.  1. -1. -1.  1.  1.  1.  1.  1.  1.  1.  1.]] 
    labels:
    [[ 1. -1.  1.  1. -1. -1.  1.  1.  1.  1.  1.  1.  1.  1.]] 
    error rate:  0.0

AUC曲线完美, 准确率也是100%.在如此数据缺失, 且特征多的情况下还能达到这么高的效果, 显示了adaboost的强大

第四部分 梯度提升(Gradient Boosting)

4.1 任意损失函数的Boosting

上一节里我们使用使用累加模型, 且损失函数为指数函数的前向分步算法实现了adaboost算法. 损失为指数函数时比较容易处理, 但其他损失函数就不是那么容易处理了.

损失函数的一般表示是: $$ L(y_i, f(x_i)) $$

考虑使用前向分步算法求解一个任意损失函数:

$$ (\beta_m, \gamma_m) = arg\min\limits_{\beta, \gamma} \sum\limits_{i=1}^N L(y_i, f_{m-1}(x_i) + \beta b(x_i;\gamma)) \tag{4.1}$$

既然 $\beta b(x_i;\gamma)$ 和 $f_{m-1}(x_i)$ 相比是等价无穷小量, 使用 泰勒级数 在 $f_{m-1}(x_i)$ 附近展开:

$$ L \approx \frac{1}{N} \sum\limits_{i=1}^N L(y_i, f_{m-1}(x_i)) + \beta \sum\limits_{i=1}^N \left. { \frac{\partial L(y_i, s)}{\partial s} } \right |_{s=f_{m-1}(x_i)} b(x_i;\gamma) \tag{4.2}$$

为 (2) 添加正则化项防止 $b(x_i;\gamma)$ 变得太大, 既然我们已经有了 $\beta$ 去调整这个项的大小了:

$$\begin{align} L & \approx \frac{1}{N} \sum\limits_{i=1}^N L(y_i, f_{m-1}(x_i)) + \frac{\beta}{2} \sum\limits_{i=1}^N \left. { 2 \frac{\partial L(y_i, s)}{\partial s} } \right |_{s=f_{m-1}(x_i)} b(x_i;\gamma) + b^2(x_i;\gamma) \\ \text{(Strip the constants)} & = \beta \sum\limits_{i=1}^N 2 \frac{\partial L}{\partial s} b(x_i;\gamma) + b^2(x_i;\gamma) \\ & = \beta \sum\limits_{i=1}^N (b(x_i;\gamma) + \frac{\partial L}{\partial s})^2 - (\frac{\partial L}{\partial s} )^2 \end{align} \tag{4.3}$$

4.2 Gradient Boosting

现在可以最小化损失函数:

  1. 求解 $b(x_i;\gamma)$. 从 (3) 可知: $$\gamma_m = arg\min\limits_\gamma \beta \sum\limits_{i=1}^N \left(b(x_i;\gamma) + \left. { \frac{\partial L(y_i, s)}{\partial s} } \right |_{s=f_{m-1}(x_i)} \right)^2$$ 也就是在每一步 $m$ 中, 利用损失函数的梯度 $-\frac{\partial L(y_i, s)}{\partial s}$ 训练基分类器 $b(x_i;\gamma_m)$. 这就是为什么它被称为梯度提升算法 $$ \text{fit } b(x_i;\gamma_m) = - \left. { \frac{\partial L(y_i, s)}{\partial s} } \right |_{s=f_{m-1}(x_i)}$$

  2. 求解 $\beta$ $$\beta_m = arg\min\limits_\beta \sum\limits_{i=1}^N L(y_i, f_{m-1}(x_i) + \beta b(x_i;\gamma_m))$$ 既然我们已经有了 $y_i$, $f_{m-1}(x_i)$ 和 $b(x_i;\gamma_m)$, 那原问题就变成了一个简单的一维变量最优化问题, 那就很容易解决了

整个算法的思想很简单, 最常用的基分类器是决策树, 称为gradient boosting decision tree (GBDT)

Updated on 2023-02-18  be87742
Read Markdown
 python
Back | Home