挺有意思的, 存在blog里参考, 以后说不定用得上. 不过这个作业应该有点历史了, 出处未考

USTC Spring 2017: Data Mining Assignment 1

SA16225220

Question 1

Classify the following attributes as binary, discrete, or continuous. Also classify them as qualitative (nominal or ordinal) or quantitative (interval or ratio). Some cases may have more than one interpretation, so briefly indicate your reasoning if you think there may be some ambiguity. Example: Age in years. Answer: Discrete, quantitative, ratio

1. Speed of a vehicle measured in mph.

• Continuous
• Quantitiative
• Ratio

Explanation: It possesses a meaningful (unique and non-arbitrary) zero value. 0 mph means motionless, 2 mph is twice as fast as 1 mph.

2. Altitude of a region.

• Continuous
• Quantitiative
• Interval

Explanation: Zero altitude is not fixed, it’s defined relatively so I’d rather take it as interval, which means at an autitude of 20m doesn’t mean it’s twice as tall as 10m.

3. Intensity of rain as indicated using the values: no rain, intermittent rain, incessant rain.

• Discrete
• Qualitative
• Ordinal

Explanation: These 3 values are comparable.

4. Brightness as measured by a light meter.

• Continuous
• Quantitiative
• Ratio

Explanation: When measured as lumen, 0 lumen means pure darkness, so it possesses a meaningful (unique and non-arbitrary) zero value.

5. Barcode number printed on each item in a supermarket.

• Discrete
• Qualitative
• Nominal

Explanation: Not comparable numbers

注: 主要是nominal, ordinal, interval 和 ratio四个measurements的比较, 其中ratio在零点有意义, interval在零点无意义所以只可相比, 没有倍数关系. 例如 20摄氏度不比10摄氏度热两倍, 但是用开尔文就可以, 所以摄氏度是interval, 开尔文是ratio

Question 2

The population for a clinical study has 500 Asian, 1000 Hispanic and 500 Native American people. What is good way of sampling this population to ensure that the distribution of various sub- populations is maintained if only 100 samples have to be chosen? Give the distribution of the various sub-populations in the final sample.

Answer:

• Asian: 25
• Hispanic: 50
• Native American: 25

注: 没啥好说的, 按比例分配样本

Question 3

Justify your answers for the following:

1. Is the Jaccard coefficient for two binary strings (i.e., string of 0s and 1s) always greater than or equal to their cosine similarity?

Answer: Assuming 2 strings could be represented as $A = (a_1, a_2, \cdots, a_n)$, $B = (b_1, b_2, \cdots, b_n)$, in which $a, b \in \lbrace 0, 1\rbrace$, then we have:

$$ J(A, B) = \frac{M_{11}}{M_{01}+M_{10}+M_{11}} = \frac{A \cdot B}{n}$$

$$cos\theta =\frac{A \cdot B}{|A||B|} \geq \frac{A \cdot B}{\sqrt{n}\sqrt{n}} = \frac{A \cdot B}{n}$$

So $$cos\theta \geq J(A, B)$$ So it’s WRONG

注: 一个意义不太大的不等式证明, 主要是介绍了二分类下的Jaccard coefficient

2. The cosine measure can range between [-1,1]. Give an example of a type of data for which the cosine measure will always be non-negative.

Answer: Since $$cos\theta =\frac{A \cdot B}{|A||B|}$$

Let $A$ & $B$ be the opposite direction, such as $$ A = -B $$ then we could always have non-negative value -1: $$ cos\theta =\frac{A \cdot (-A)}{|A||-A|} = -1 $$

注: 只要两个向量夹角是钝角就行了. 高中知识.

Question 4

The similarity between two undirected graphs G1 and G2 that have the same n vertices can be defined using: $$ S(G_1, G_2) = \frac{\sum_i min(deg(v_i \in G_1), deg(v_i \in G_2))}{2 \times max(|G_1|, |G_2|)} $$ where $deg(v ∈ G)$ indicates the degree of a vertex $v$ in graph $G$ and $|G|$ indicates the number of edges in $G$. If $S(G1, G2) = 1$, are the two graphs equivalent? Provide an example to justify your answer.

Answer: No. Example: 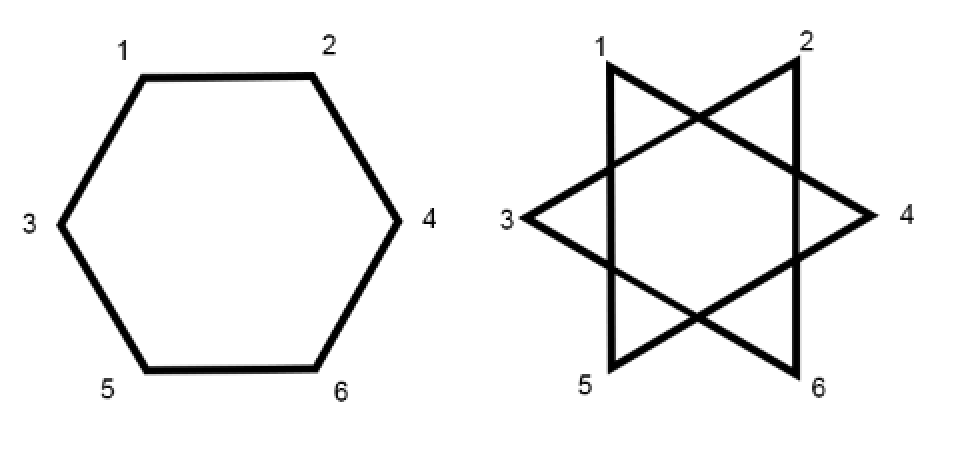Same degree for each vertex, same number of edges in each graph, $S(G_1, G_2) = \frac{12}{12} = 1$, but the two graphs are not equivalent.

注: 每个顶点的度数相同, 边也相同那么这里的相似度就是1, 但两个图并不一定一样. 只要举个反例就行了.

Question 5

For every item i in a grocery store, a set $s_i$ is used to represent the IDs of transactions in which $i$ is purchased. Assume that the data set to be analyzed contains hundreds of thousands of such transactions.

1. In order to analyze the proximity between any two of these sets $s_i$ and $s_j$, which measure, Jaccard or Hamming, would be more appropriate and why ?

Answer: Since we want to find the similarity between 2 sets, Jaccard coefficient is more preferable.

2. In order to analyze the proximity between any two of these sets $s_i$ and $s_j$ for items i and j that are often brought together (example: milk, bread), which measure, Jaccard or Hamming, would be more appropriate and why ?

Answer: Since item $i$ and $j$ that are often brought together, they have high similarity, then we should focus on the difference between these 2 sets. So Hamming distance is more preferable.

注: Jaccard主要关心相似度, Hamming主要关注不同, 知道这点这题就没什么了. 注意这两者的适用背景即可.

Question 6

For the data set described below, give an example of the types of data mining questions that can be asked (one for each classification, clustering, association rule mining, and anomaly detection task) and the description of the data matrix (what are the rows and columns). If necessary, briefly explain the features that need to be constructed. Note that, depending on your data-mining question, the row and column definitions may be different.

A clinical dataset containing various measures like temperature, blood pressure, blood glucose and heart rate for each patient during every visit, along with the diagnosis information.

Answer:

DM Task: Classification of disease
Question: Which disease does the patient have?
Row: The body measures of a patient.
Column: Temperature, blood pressure, blood glucose, heart rate, etc. for each patient.

DM Task: Clustering similar patients
Question: What are the patients with similar disease?
Row: A patient’s diagnosis information.
Column: Temperature, blood pressure, blood glucose, heart rate, etc. for each patient.

DM Task: Association rule mining
Question: What are the diseases tend to appear together? For example, high blood pressure and heart attack.
Row: A patient’s diagnosis information.
Column: Diagnosis information, especially the disease names.

DM Task: Anomaly detection
Question: Is the patient’s body measures mistaken? For example, mistaken by typo during input, like temperature = 50℃
Row: The body measures of a patient.
Column: Temperature, blood pressure, blood glucose, heart rate, etc. for each patient.

注: 主要是举点数据挖掘例子

---

USTC Spring 2017: Data Mining Homework 2

Question 1

[30 points: 5 for each part] Consider the training examples shown in Table 1 for a binary classification problem.

• (a) Compute the Entropy for the overall collection of training examples. Answer: $$\begin{align} H(Class) &= -\sum_{C0,C1} (P_{C0}logP_{C0} + P_{C1}logP_{C1}) \\ & = -(0.5log0.5 + 0.5log0.5) \\ &= 1 \end{align}$$

• (b) Compute the Entropy for the Movie ID attribute. Answer: Each Movie ID has its distinct number of ID, so apparently it has no contribution to the infomation gain of Class, so $$H(Class | Movie ID) = 0$$

• (c) Compute the Entropy for the Format attribute. Answer: $$\begin{align} & H(Class | Format = DVD) \\ &= -\sum_{C0,C1} (P_{C0, DVD}logP_{C0, DVD} + P_{C1, DVD}logP_{C1, DVD}) \\ & = -(\frac{6}{8}log\frac{6}{8} + \frac{2}{8}log\frac{2}{8}) \\ &= 0.8112 \end{align}$$ $$\begin{align} & H(Class | Format = Online) \\ &= -\sum_{C0,C1} (P_{C0, Online}logP_{C0, DVD} + P_{C1, Online}logP_{C1, Online}) \\ & = -(\frac{4}{12}log\frac{4}{12} + \frac{8}{12}log\frac{8}{12}) \\ &= 0.9182 \end{align}$$ $$ \begin{align} & H(Class|Format)\\ & = P_{DVD}H(Class | DVD) + P_{Online}H(Class | Online) \\ & = \frac{8}{20} \times 0.8112 + \frac{12}{20} \times 0.9182 \\ & = 0.8754 \end{align} $$

• (d) Compute the Entropy for the Movie Category attribute using multiway split. Answer: $$\begin{align} & H(Class | Entertainment) \\ &= -\sum_{C0,C1} (P_{C0, En}logP_{C0, En} + P_{C1, En}logP_{C1, En}) \\ & = -(\frac{1}{4}log\frac{1}{4} + \frac{3}{4}log\frac{3}{4}) \\ &= 0.8112 \end{align}$$ Similarly, $$ H(Class | Comedy) = 0.5435 \\ H(Class | Documentation) = 0.8112 $$ So $$ \begin{align} & H(Class| Movie Category)\\ & = P_{En}H(Class | En) + P_{Com}H(Class | Com) + P_{Doc}H(Class | Doc)\\ & = 0.2 \times 0.81125 + 0.4 \times 0.5435+ 0.4 \times 0.81125 \\ & = 0.7042 \end{align} $$

• (e) Which of the three attributes has the lowest Entropy? Answer: Movie ID which is 0

• (f) Which of the three attributes will you use for splitting at the root node? Briefly explain your choice. Answer: As for infomation gain, $$\begin{align} H(Class) - H(Class|Movie ID) & = 1 \\ H(Class) - H(Class|Format) & = 1 - 0.8754 = 0.125 \\ H(Class) - H(Class|Movie Category) & = 1 - 0.7042 = 0.296 \end{align} $$ Choose Movie Category is better because it has more info gain, although Movie ID has the most infomation gain (1), but it has overfitting.

注: 关于条件熵和信息增益, 参考之前的blog

Question 2

[19 points: 6+5+8] Consider the decision tree shown in Figure 1, and the corresponding training and test sets in Tables 2 and 3 respectively.

• (a) Estimate the generalization error rate of the tree using both the optimistic approach and the pessimistic approach. While computing the error with pessimistic approach, to account for model complexity, use a penalty value of 2 to each leaf node. Answer: Optimistic error rate: 0 Pessimistic error rate: $$ ErrorRate = \frac {e(T) + \Omega(T)}{N_t} = \frac{0 + 6 \times 2}{15} = 0.8$$

• (b) Compute the error rate of the tree on the test set shown in Table 3 Answer: Since (0,0,0,0) and (0,0,0,1) are wrong, $$ ErrorRate = \frac{4+3}{15} = 0.47$$

• (c) Comment on the behaviour of training and test set errors with respect to model complex- ity. Comment on the utility of incorporating model complexity in building a predictive model. Answer:

  • With model complexity increasing, the performance of the model will increase on the training set but decrease on the testing set
  • Pruning the data through pessimistic error rate will get a better performance on testing set, as well as a simpler model, less computing complexity.

注: 关于剪枝的判断, 主要是叶节点个数(复杂度)和分类错误率

Question 3

[20 points: 10 for each part] Given the data sets shown in Figure 2, explain how the decision tree and k-nearest neighbor (k-NN) classifiers would perform on these data sets.

Answer:

1. Decision tree: Discriminating attributes and noise attributes make decision tree prone to overfitting
2. k-NN: If k is too big, it will label the central samples as A rather than B, which is the right label.

Question 4

[16 points: 4 for each part] Consider the problem of predicting if a given person is a defaulted borrower (DB) based on the attribute values:

• Home Owner = Yes, No
• Marital Status = Single, Married, Divorced
• Annual Income = Low, Medium, High
• Currently Employed = Yes, No

Suppose a rule-based classifier produces the following rules:

• Home Owner = Yes → DB=Yes
• Marital Status = Single → DB = Yes
• Annual Income = Low → DB = Yes
• Annual Income = High, Currently Employed = No → DB = Yes
• Annual Income = Medium, Currently Employed = Yes → DB = No
• Home Owner = No, Marital Status = Married → DB = No
• Home Owner = No, Marital Status = Single → DB = Yes

Answer the following questions. Make sure to provide a brief explanation or an example to illustrate the answer.

• (a) Are the rules mutually exclusive ? Answer: No. Example: Home Owner = No, Marital Status = Single, Annual Income = Low/High → DB = Yes
• (b) Is the rule set exhaustive ? Answer: No. There is no rule for Marital Status = Divorced
• (c) Is ordering needed for this set of rules ? Answer: Better have an order to avoid conflict: Home Owner, Marital Status, Annual Income, Currently Employed
• (d) Do you need a default class for the rule set ? Answer: Yes, since it’s not set exhaustive.

注: 基于规则的方法

Question 5

[15 points] Consider the problem of predicting whether a movie is popular given the following attributes: Format (DVD/Online), Movie Category (Comedy/Documentaries), Release Year, Number of world-class stars, Director, Language, Expense of Production and Length. If you had to choose between RIPPER and a k-nearest neighbor classifier, which would you prefer and why? Briefly explain why the other one may not work so well?

Answer: I’d prefer RIPPER.

• RIPPER is a rule based method. It has a good performance on noisy and unbalanced data. Apparently the number of popular films is far less than the non-popular ones so the training set would be unbalanced as well as noisy.
• Since the attributes has different types and the number of attributes is relatively big, using k-NN would couse overfitting on the training set if its popularity is not large enough, or even fail to have reasonable cluster if the feature space is too sparse. (like empty cluster, etc.)