Neural Networks Learning
Cost Fuction
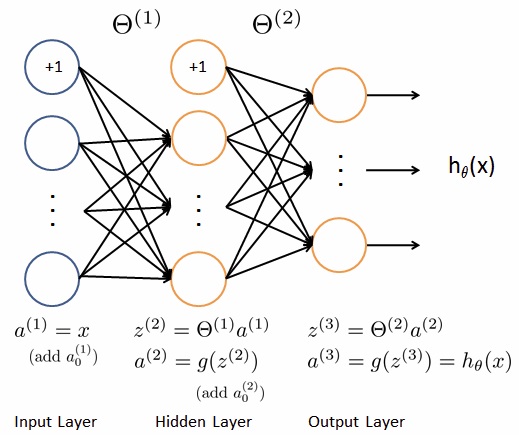
1. For a neural network like the pic above, the cost function should be like:
$$
J(\theta) = \frac {1}{m} \sum\limits\_{i=1}^{m}\sum\limits\_{k=1}^{K}
[-y\_k^{(i)} log(h\_\theta (x^{(i)})\_k) - (1 - y\_k^{(i)}) log(1 - h\_\theta (x^{(i)})\_k)]
$$
2. In which there are m training data and the output layer has K units. The cost function will sum all the outputs from all the data.
3. Similarly, the regularization term just sum up the square of all the parameters from all the layers:
$$
\frac {\lambda}{2m}
\sum\limits\_{j=1}^{s^{(l)}}
\sum\limits\_{k=2}^{s^{(l+1)}}
\sum\limits\_{l=1}^{n}
[(\Theta\_{jk}^{(l)})^2]
$$
4. Note that you should not be regularizing the terms that correspond to the bias. For the matrices here, this corresponds to the first column of each matrix, so k should start from index 2.
Backpropagation Algorithm

1. In order to use optimization algorithms like gradient descent, we must calculate the derivative of the cost function. First we should calculate $\delta$ for each layer using backpropagation algorithm. From $layer\_l$ to $layer\_{l+1}$, we have:
$$
\delta^{(output)} = a^{(output)} - y
\\\
\delta^{(l)} = [\Theta^{(l)}]^T \delta^{(l+1)} .* g'(z^{(l)})
$$
2. For sigmoid function, $g'(z) = g(z)(1-g(z))$
3. Then we have the derivative:
$$
\frac {\partial}{\partial \Theta\_{ij}^{(l)}} J(\Theta) = a\_j^{(l)} \delta\_i^{(l+1)} \\\
\Delta^{(l)} = \delta^{(l+1)} (a^{(l)})^T
$$
4. Instead of calculate the $\Delta$ for all the training data, we could sum up all the inputs independantly, like:
$$
\begin{align}
& \text{From i = 1 to m, do:} \\\
&& \Delta^{(l)} += \delta^{(l+1)} (a^{(l)})^T \\\
& \text{Then we have:} \\\
&& \frac {\partial}{\partial \Theta\_{ij}^{(l)}} J(\Theta) = \frac {1}{m} \Delta\_{ij}^{(l)}
\end{align}
$$
- (This step is the main step for mapreduce, see Large Scale Machine Learning)
5. Then add regularzation term for partial derivative, we have:
$$
\frac {\partial}{\partial \Theta\_{ij}^{(l)}} J(\Theta) = \frac {1}{m} \Delta\_{ij}^{(l)} + \frac {\lambda}{m} \Theta\_{ij}^{(l)}
$$
6. Finally, using $J(\Theta)$ and $\frac {\partial}{\partial \Theta\_{ij}^{(l)}} J(\Theta)$, we could minimize the cost function using gradient descent as well as other optimization algorithms.
Optional Section: How Backpropagation Works
Using the same model as the last section:
$$
\begin{align}
\frac {\partial J}{\partial \Theta_{ij}^{(1)}} & =
\frac {\partial J}{\partial a_i^{(2)}}
\frac {\partial a_i^{(2)}}{\partial z_i^{(2)}}
\frac {\partial z_i^{(2)}}{\partial \Theta_{ij}^{(1)}} \\ & =
\frac {\partial J}{\partial a_i^{(2)}} g’(z_i^{(2)}) a_i^{(1)}
\end{align}
$$
Then taking the total derivative with respect to $z^{(3)}$, a recursive expression for the derivative is obtained:
$$
\begin{align}
\frac {\partial J}{\partial a_i^{(2)}} & =
\sum\limits_{m=1}^{s_3}
\frac {\partial J}{\partial z_m^{(3)}}
\frac {\partial z_m^{(3)}}{\partial a_i^{(2)}} \\ & =
\sum\limits_{m=1}^{s_3}
\frac {\partial J}{\partial a_m^{(3)}}
\frac {\partial a_m^{(3)}}{\partial z_m^{(3)}}
\frac {\partial z_m^{(3)}}{\partial a_i^{(2)}} \\ & =
\sum\limits_{m=1}^{s_3}
\frac {\partial J}{\partial a_m^{(3)}} g’(z_m^{(3)}) \Theta_{mi}^{(2)}
\end{align}
$$
Let $
\delta_i^{(2)} =
\frac {\partial J}{\partial a_i^{(2)}} g’(z_i^{(2)})
$, then from the result of the first formula We have: $
\frac {\partial J}{\partial \Theta_{ij}^{(1)}} =
\delta_i^{(2)} a_i^{(1)}
$, in which recursively, $
\delta_i^{(2)} =
(\sum\limits_{m=1}^{s_3}
\delta_m^{(3)}\Theta_{mi}^{(2)}) g’(z_i^{(2)})
$
Referance: http://www.wikiwand.com/en/Backpropagation#Derivation

