吴恩达 ML 公开课笔记(6)-Logistic Regression

Logistic Regression

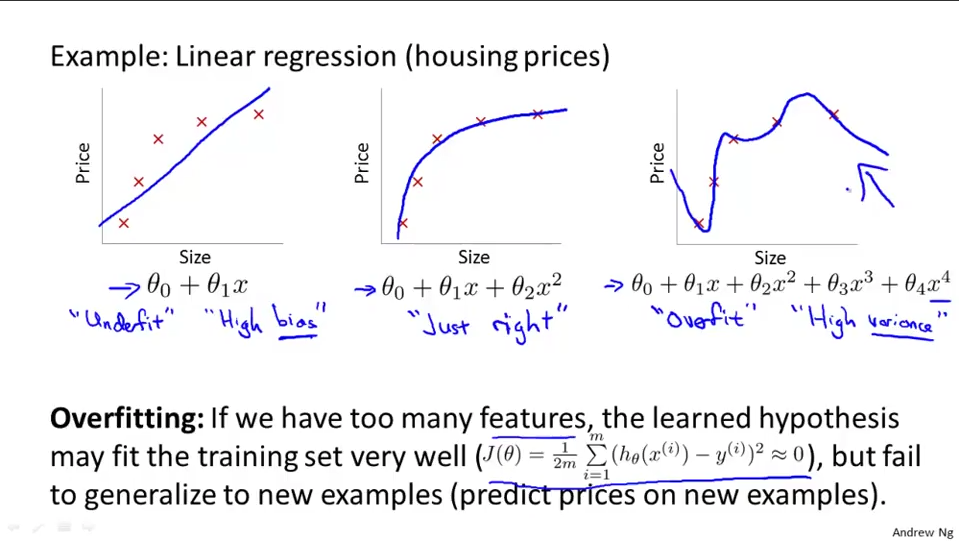
Linear Regression is not suitable for classification problem

• overfit
• $h_\theta$ can be >1 or <0

Logisitc Regression

1. Hypothesis Representation
   • Sigmoid/Logistic Function for linear regression: $$h_\theta (x) = \frac {1}{1 + e^{-\theta^T x}}$$
   • Interpretation: estimated probability that y=1 on input x
   • $P(y=0|x=\theta) + P(y=1|x=\theta) = 1$
2. Decision Boundary
   • Linear Regression: y=1 equals to $\theta^T x$ > 0 which is decided by parameters
   • Unlinear Regression: Polynomial Regression etc.
3. Cost function for one variable hypothesis
   • To let the cost function be convex for gradient descent, it should be like this: $$Cost(h_\theta (x), y) = \begin{cases} -log(h_\theta (x)), & (y = 1) \\ -log(1 - h_\theta (x)), & (y = 0) \\ \end{cases}$$
4. Simplified Cost Function
   • $Cost(h_\theta (x), y) = y log(h_\theta (x)) + (1 - y)log(1 - h_\theta (x))$
   • For a set of training data, we have: $$ J(\theta) = -\frac{1}{m}\sum\limits_{i=1}^{m}[y^{(i)}\log h_\theta(x^{(i)}) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] $$
5. Minimize $J(\theta)$ using gradient descent $$\frac{\partial}{\partial \theta_j} J(\theta) = \frac{1}{m}\sum\limits_{i=1}^{m}[(h_\theta (x^{(i)}) - y^{(i)})x_j^{(i)}]$$ $$\theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}[(h_\theta (x^{(i)}) - y^{(i)})x_j^{(i)}]$$
6. Advanced Optimization
   • Other optimization algorithms other than gradient descent (do not need to manually pick $\alpha$):
     • Conjugate descent
     • BGFS
     • L-BFGS
7. Multiclass Classification: One-vs-all
   • For more than 2 features of y, do logisitc regression for each feature separately

Regularzation

1. The problem of overfitting
   • 
   • 
2. Addressing overfitting
   • Reduce number of features (manually/model selection)
   • Regularzation: add panalize terms to some less important parameters, or panalize all the parameters(except for $\theta_0$)
3. Regularized Linear Regression $$\displaystyle \theta_j := \theta_j(1-\alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j$$
   • For normal equation, regularization would also make $X^T X$ invertible
4. Regularized Logistic Regression
   • Literally the same as Regularized Linear Regression except for the form of $h_\theta (x)$